Решение С3 ЕГЭ по Математике
Задание, которое я сегодня разберу, представляет собой систему 2 неравенств, одно из которых показательное 25x 3*10x-4*4x>0, а другое логарифмическое
log1-x2/37(x2-12|x| 37)-log1 x2/37(x2-12|x| 37)>=0
Любое задание С3 решается по следующей схеме: сначала мы находим решение первого неравенства, затем второго, и наконец составляем систему из решений обеих неравенств - записываем ответ.
Первое неравенство мы приводим к квадратному неравенству делая замену (5/2)x=t.

Во втором неравенстве находим ОДЗ, одно слагаемое переносим за знак. Обе части раскладываем методом рационализации и решаем квадратное неравенство с модулем. Оно всегда положительное и равно нулю только при x=6.
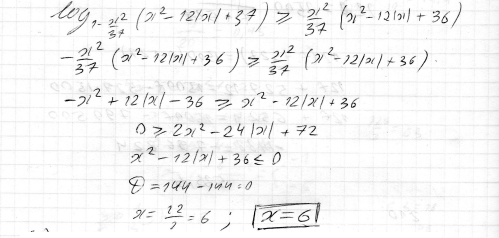
Получаем общий ответ: 6
log1-x2/37(x2-12|x| 37)-log1 x2/37(x2-12|x| 37)>=0
Любое задание С3 решается по следующей схеме: сначала мы находим решение первого неравенства, затем второго, и наконец составляем систему из решений обеих неравенств - записываем ответ.
Первое неравенство мы приводим к квадратному неравенству делая замену (5/2)x=t.

Во втором неравенстве находим ОДЗ, одно слагаемое переносим за знак. Обе части раскладываем методом рационализации и решаем квадратное неравенство с модулем. Оно всегда положительное и равно нулю только при x=6.
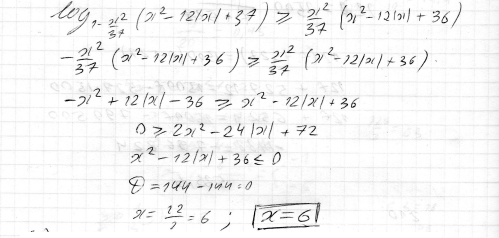
Получаем общий ответ: 6
Просмотры: 5182 |
Статью добавил: slava191 |
Категория: математика
☰ Меню