Тригонометрия, или как решать задания 13 единого государственного экзамена по математике. Часть II.

Сейчас мы рассмотрим такую тему в тригонометрии, как формулы приведения и изучим несколько способов их применения и запоминания.

1. Первый способ вывода формул приведения - это использования формул:





Чтобы посчитать например cos(Pi/2+x) представим Pi/2 как α, a x как β.

И распишем по формуле косинуса суммы, получим:



Все что нужно для этого способа - это знание этой формулы, и значения косинусов и синусов частного угла.

2. К счастью для ленивых есть более быстрый и удобный способ использования формул приведения. Для этого нужно вспомнить нашу окружность.

Рассмотрим малый угол X его косинус будет равен cos(x), а синус sin(x). Повернем наш угол на 90 градусов против часовой стрелки. Теперь угол наклона новой прямой стал равен (Pi/2+x) (это хорошо заметно на нашем рисунке).



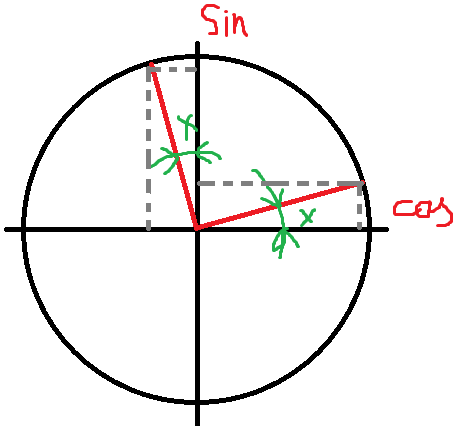
Самым важным является то, что из рисунка видно, что cos(x)=sin(Pi/2+x) (это следует хотя бы из равенства треугольников) а sin(x)=-cos(x). Получается для того, чтобы использовать формулы приведения нужно только представить себе нужный угол, и из рисунка (воображения) понять чему равен тот или иной косинус.

3. Некоторых в школе учат простым мнемоническим правилам.

Они говорят, что если в формуле приведения есть Pi/2 то косинус меняется на синус, а синус на косинус. Знак же определяется той четвертью в которой находится угол изначально.

Для понимания приведу простой пример: пусть будет sin(Pi/2+x). Т.к. есть Pi/2, то синус сменится на косинус. Теперь необходимо понять в какой степени находится Pi/2+x (х - это малый угол, из-за чего нельзя определить четверть двояко).

Pi/2+x это вторая четверть, синус в которой положителен, следовательно знак не изменится, получается sin(Pi/2+x)=cos(x).

(Важное замечание к этому методу! Знак мы определяем по первоначальной функции, в нашем случае по синусу, если бы изначально был cos(Pi/2+x), то знак определялся бы по косинусу.).