Тригонометрия, или как решать задания 13 единого государственного экзамена по математике. Часть I.

Начну свою первую статью с определения синуса и косинуса. Изначально эти понятия были введены для прямоугольного треугольника, где синусом называли число, сопоставляемое углу, равное отношению противолежащего катета к гипотенузе. А косинусом, число сопоставляемое углу и равное отношению прилежащего катета к гипотенузе.



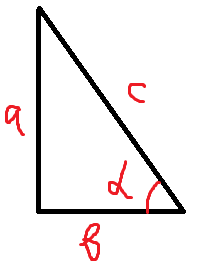
Тангенс это отношение синуса к косинусу, а котангенс это отношение косинуса к синусу.

Теперь перейдем к самому важному, это к тригонометрической единичной окружности, это окружность радиуса 1.



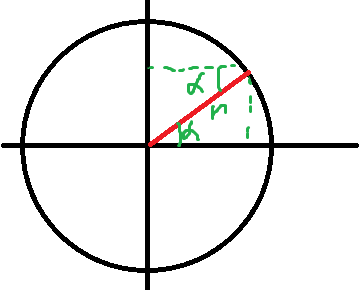
И рассмотрим произвольную прямую под углом альфа. r=1 т.к. радиус у нас равен одному. Заметим, что проекция на горизонталь у нас равна r*cosa а т.к. r=1. то и горизонтальная проекция является просто косинусом. Также вертикальная ось является синусом (по тем же соображениям, чтобы удостовериться просто распишите синус для нашего треугольника). Также мы можем записать Теорему Пифагора для нашего треугольника из чего получим: sin^2(a)+cos^2(a)=1 эту формулу называют основным тригонометрическим тождеством, из этой формулы, зная синус можно узнать косинус и наоборот.

Также важными формулами в тригонометрии являются:

Синус суммы:



Косинус суммы:



Тангенс и котангенс суммы можно получить поделив эти формулы друг на друга. Но даже это вряд ли пригодится для ЕГЭ.

Формулы двойных и тройных углов выводятся из формул (1) и (2) :