Отбор корней в тригонометрическом уравнение
В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение √2cos2x=sin(π/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [–7π/2; –2π]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(π/2+x) = cos(x)
√2cos2x = cosx
√2cos2x – cosx = 0
cosx(√2cosx – 1) = 0
cosx = 0
x1 = π/2 + πn, n ∈ Z
√2cosx – 1 = 0
cosx = 1/√2
cosx = √2/2
x2 = arccos(√2/2) + 2πn, n ∈ Z
x3 = –arccos(√2/2) + 2πn, n ∈ Z
x2 = π/4 + 2πn, n ∈ Z
x3 = –π/4 + 2πn, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [–7π/2; –2π], находим целые значения для n.
–7π/2 ≤ π/2 + πn ≤ –2π
Сразу делим все на π
–7/2 ≤ 1/2 + n ≤ –2
–7/2 – 1/2 ≤ n ≤ –2 – 1/2
–4 ≤ n ≤ –5/2
Целые n в этом промежутку это –4 и –3. Значит корни принадлежащие этому промежутку буду π/2 + π(–4) = –7π/2, π/2 + π(–3) = –5π/2
Аналогично делаем еще два неравенства
–7π/2 ≤ π/4 + 2πn ≤ –2π
–15/8 ≤ n ≤ –9/8
Целых n в этом промежутке нет
–7π/2 ≤ –π/4 + 2πn ≤ –2π
–13/8 ≤ n ≤ –7/8
Одно целое n в этом промежутку это –1. Значит отобранный корень на этом промежутку –π/4 + 2π·(–1) = –9π/4.
Значит ответ в пункте б: –7π/2, –5π/2, –9π/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
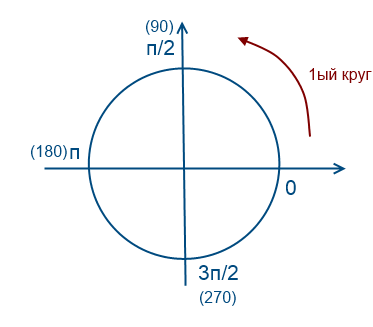
Обойдем раз против часовой стрелки
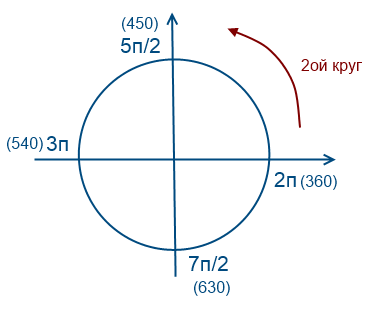
Обойдем 2 раза против часовой стрелки
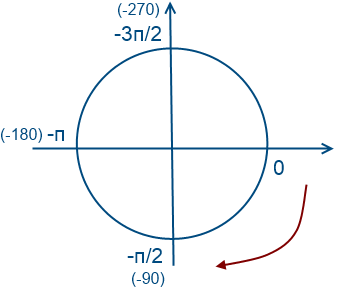
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
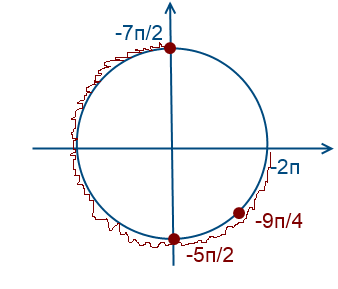
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [–7π/2; –2π]
Чтобы попасть к числам –7π/2 и –2π надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = π/2 + πn. Какой приблизительно должен быть n, чтобы значение x было где–то в этом промежутке? Подставляем, допустим –2, получаем π/2 – 2π = –3π/2, очевидно это не входит в наш промежуток, значит берем меньше –3, π/2 – 3π = –5π/2, это подходит, попробуем еще –4, π/2 – 4π = –7π/2, также подходит.
Рассуждая аналогично для π/4 + 2πn и –π/4 + 2πn, находим еще один корень –9π/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
б) Найдите все корни этого уравнения, принадлежащие промежутку [–7π/2; –2π]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(π/2+x) = cos(x)
√2cos2x = cosx
√2cos2x – cosx = 0
cosx(√2cosx – 1) = 0
cosx = 0
x1 = π/2 + πn, n ∈ Z
√2cosx – 1 = 0
cosx = 1/√2
cosx = √2/2
x2 = arccos(√2/2) + 2πn, n ∈ Z
x3 = –arccos(√2/2) + 2πn, n ∈ Z
x2 = π/4 + 2πn, n ∈ Z
x3 = –π/4 + 2πn, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [–7π/2; –2π], находим целые значения для n.
–7π/2 ≤ π/2 + πn ≤ –2π
Сразу делим все на π
–7/2 ≤ 1/2 + n ≤ –2
–7/2 – 1/2 ≤ n ≤ –2 – 1/2
–4 ≤ n ≤ –5/2
Целые n в этом промежутку это –4 и –3. Значит корни принадлежащие этому промежутку буду π/2 + π(–4) = –7π/2, π/2 + π(–3) = –5π/2
Аналогично делаем еще два неравенства
–7π/2 ≤ π/4 + 2πn ≤ –2π
–15/8 ≤ n ≤ –9/8
Целых n в этом промежутке нет
–7π/2 ≤ –π/4 + 2πn ≤ –2π
–13/8 ≤ n ≤ –7/8
Одно целое n в этом промежутку это –1. Значит отобранный корень на этом промежутку –π/4 + 2π·(–1) = –9π/4.
Значит ответ в пункте б: –7π/2, –5π/2, –9π/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [–7π/2; –2π]
Чтобы попасть к числам –7π/2 и –2π надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = π/2 + πn. Какой приблизительно должен быть n, чтобы значение x было где–то в этом промежутке? Подставляем, допустим –2, получаем π/2 – 2π = –3π/2, очевидно это не входит в наш промежуток, значит берем меньше –3, π/2 – 3π = –5π/2, это подходит, попробуем еще –4, π/2 – 4π = –7π/2, также подходит.
Рассуждая аналогично для π/4 + 2πn и –π/4 + 2πn, находим еще один корень –9π/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
Просмотры: 174937 |
Статью добавил: slava191 |
Категория: математика
☰ Меню