Задача 76713 Найти частное решение дифференциального...
Условие
удовлетворяет начальному условию.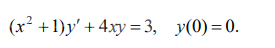
Решение
Делим всё уравнение на (x^2 + 1)
y' + 4xy/(x^2 + 1) = 3/(x^2 + 1)
Неоднородное уравнение 1 порядка, решается заменой:
y = u*v; y' = u'*v + u*v'
u'*v + u*v' + 4x*uv/(x^2 + 1) = 3/(x^2 + 1)
Выносим u за скобки во 2 и 3 слагаемых:
u'*v + u*(v' + 4x*v/(x^2 + 1)) = 3/(x^2 + 1)
Приравниваем скобку к 0:
v' + 4x*v/(x^2 + 1) = 0
dv/dx = -4x*v/(x^2 + 1)
dv/v = -4x/(x^2 + 1)*dx
Уравнение с разделенными переменными, интегрируем:
[m]\int \frac{dv}{v} = \ln |v|[/m]
[m]\int \frac{-4x}{x^2 + 1}dx = -2 \int \frac{2xdx}{x^2 + 1} = -2 \int \frac{d(x^2+1)}{x^2 + 1} = -2\ln |x^2 + 1| = ln |\frac{1}{(x^2 + 1)^2}|[/m]
Получаем:
[m]\ln |v| = ln |\frac{1}{(x^2 + 1)^2}|[/m]
[m]v = \frac{1}{(x^2 + 1)^2}[/m]
Подставляем в уравнение:
u'*v + u*(v' + 4x*v/(x^2 + 1)) = 3/(x^2 + 1)
[m]u' \cdot \frac{1}{(x^2 + 1)^2} + u \cdot 0 = \frac{3}{x^2 + 1}[/m]
[m]u' \cdot \frac{1}{(x^2 + 1)^2} = \frac{3}{x^2 + 1}[/m]
Умножаем всё уравнение на (x^2 + 1)^2:
u' = 3(x^2 + 1)
u = 3(x^3/3 + x) + C = x^3 + 3x + C
Возвращаемся к функции y = u*v:
[b]y = (x^3 + 3x + C)/(x^2 + 1)^2[/b]
Теперь подставляем начальные условия y(0) = 0:
y(0) = (0 + 3*0 + C)/(0 + 1)^2 = C/1^2 = C = 0
[b]y = (x^3 + 3x)/(x^2 + 1)^2[/b]