Задача 75961 решить интеграл номер 16,17,18...
Условие

Решение

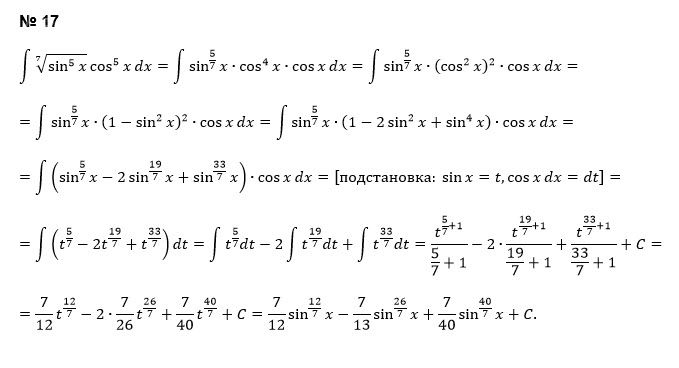

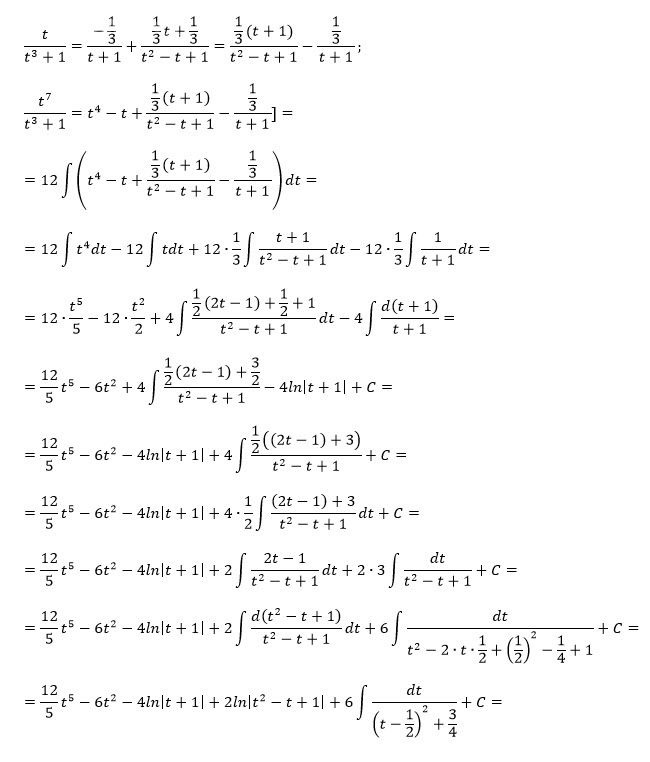
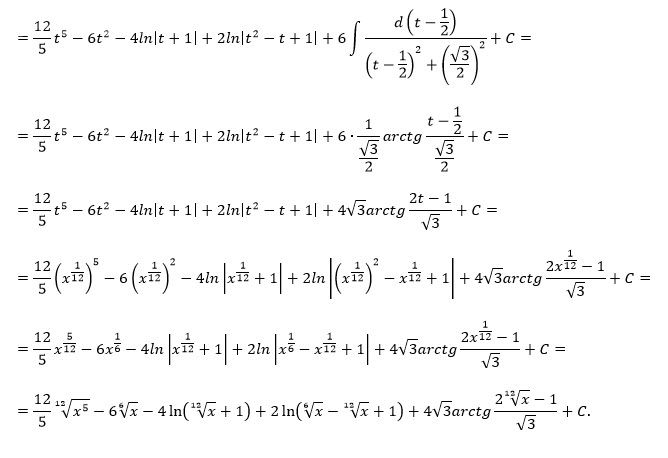
Все решения
Преобразуем
cos 2x = 1 - 2sin^2 (x); отсюда sin^2 (x) = 1/2*(1 - cos 2x). Поэтому:
sin^6 (2x) = (sin^2 (2x))^3 = (1/2*(1 - cos 4x))^3 = 1/8*(1 - cos 4x)^3
sin^6 (2x) = 1/8*(1 - 3cos 4x + 3cos^2 4x - cos^3 4x)
Далее, cos 2x = 2cos^2 x - 1, отсюда cos^2 x = 1/2*(1 + cos 2x). Поэтому:
3cos^2 (4x) = 3/2*(1 + cos 8x)
cos^3 (4x) = cos(4x)*cos^2 (4x) = cos(4x)(1/2*(1 + cos 8x)) =
= 1/2*(cos 4x + cos 4x*cos 8x) = 1/2*(cos 4x + 1/2*(cos(8x-4x) + cos(8x+4x))) =
= 1/2*cos 4x + 1/4*cos 4x + 1/4*cos 12 x = 3/4*cos 4x + 1/4*cos 12x
Итого получаем:
sin^6 (2x) = 1/8*(1 - 3cos 4x + 3cos^2 4x - cos^3 4x) =
= 1/8*(1 - 3cos 4x + 3/2*(1 + cos 8x) - (3/4*cos 4x + 1/4*cos 12x)) =
= 1/8 - 3/8*cos 4x + 3/16 + 3/16*cos 8x - 3/32*cos 4x - 1/32*cos 12x =
= 5/16 - 15/32*cos 4x + 3/16*cos 8x - 1/32*cos 12x
Теперь берем интеграл:
[m]16 \int \sin^6(2x) dx = 16 \int (\frac{5}{16} - \frac{15}{32}cos 4x + \frac{3}{16}cos 8x - \frac{1}{32}cos 12x) dx = \int (5 - \frac{15}{2}cos(4x) + 3cos(8x) - \frac{1}{2}cos(12x)) dx =[/m]
[m]= 5x - \frac{15}{2}\frac{1}{4}sin(4x) + 3 \cdot \frac{1}{8}sin(8x) - \frac{1}{2}\frac{1}{12}sin(12x)+C= 5x - \frac{15}{8}sin(4x) + \frac{3}{8}sin(8x) - \frac{1}{24}sin(12x)+C[/m]
18) [m]\int \frac{dx}{(1+\sqrt[4]{x})\sqrt[3]{x}}[/m]
Замена [m]y=\sqrt[12]{x}; \sqrt[4]{x} = y^3; \sqrt[3]{x} = y^4[/m], тогда [m]x=y^{12}; dx = 12y^{11} dy[/m]
[m]\int \frac{dx}{(1+\sqrt[4]{x})\sqrt[3]{x}} = \int \frac{12y^{11} dy}{(1+y^3)y^4}=12\int \frac{y^7}{1+y^3}dy=[/m]
[m]= 12\int \frac{y^7+y^4-y^4-y+y}{1+y^3}dy = 12\int \frac{y^4(y^3+1)-y(y^3+1)+y}{1+y^3}dy = 12\int (y^4 - y + \frac{y}{1+y^3})dy =[/m]
[m]= 12(\frac{y^5}{5} - \frac{y^2}{2} + \int \frac{y}{1+y^3}dy)[/m]
Последний интеграл решается методом неопределенных коэффициентов. Он равен:
[m]\int \frac{y}{1+y^3}dy = \frac{1}{6}(ln|y^2-y+1| - 2ln|y+1| + 2\sqrt{3} \cdot arctg(\frac{2y-1}{\sqrt{3}}))+C[/m]
В итоге:
[m]12(\frac{y^5}{5} - \frac{y^2}{2} + \int \frac{y}{1+y^3}dy) = 12(\frac{y^5}{5} - \frac{y^2}{2} + \frac{1}{6}(ln|y^2-y+1| - 2ln|y+1| + 2\sqrt{3} \cdot arctg(\frac{2y-1}{\sqrt{3}})))+C[/m]
Возвращаемся к x:
[m]\int \frac{dx}{(1+\sqrt[4]{x})\sqrt[3]{x}} =12(\frac{\sqrt[12]{x^5}}{5} - \frac{\sqrt[6]{x}}{2} + \frac{1}{6}(ln|\sqrt[6]{x}-\sqrt[12]{x}+1| - 2ln|\sqrt[12]{x}+1| + 2\sqrt{3} \cdot arctg(\frac{2\sqrt[12]{x}-1}{\sqrt{3}})))+C[/m]