Задача 75494 Решить уравнения комбинаторики...
Условие
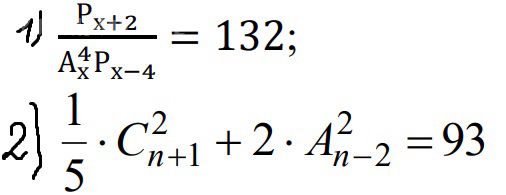
Решение
Во-первых, x ≥ 0, в комбинаторике всегда так.
Перепишем так:
[m]\frac{P_{x+2}}{P_{x-4}} \cdot \frac{1}{A^4_{x}} = 132[/m]
P - это перестановки, P_(n) = n! (факториал числа n).
A - это размещения, A^(m)_(n) = n!/(n-m)!
В нашем случае:
[m]\frac{P_{x+2}}{P_{x-4}} \cdot \frac{1}{A^4_{x}} = \frac{(x+2)!}{(x-4)!} \cdot \frac{(x-4)!}{x!} = 132[/m]
[m]\frac{(x+2)!}{x!}= 132[/m]
[m]\frac{x!(x+1)(x+2)}{x!} = (x+1)(x+2) = 132[/m]
Решаем квадратное уравнение:
x^2 + 3x + 2 = 132
x^2 + 3x - 130 = 0
D = 3^2 - 4*(-130) = 9 + 520 = 529 = 23^2
Так как x ≥ 0, то подходит только один корень:
x = (-3 + 23)/2 = 20/2 = 10
2) [m]\frac{1}{5} \cdot C^2_{n+1} + 2 \cdot A^2_{n-2} = 93[/m]
C - это сочетания, [m]C^{m}_{n} = \frac{n!}{m!(n-m)!}[/m]
В нашем случае:
[m]\frac{1}{5} \cdot \frac{(n+1)!}{2!(n+1-2)!} + 2 \cdot \frac{(n-2)!}{(n-2-2)!} = 93[/m]
[m]\frac{(n+1)!}{5 \cdot 2(n-1)!} + \frac{2(n-2)!}{(n-4)!} = 93[/m]
[m]\frac{(n-1)! \cdot n(n+1)}{10(n-1)!} + \frac{2(n-4)!(n-3)(n-2)}{(n-4)!} = 93[/m]
[m]\frac{n(n+1)}{10} + 2(n-3)(n-2) = 93[/m]
Домножим всё на 10 и избавимся от дробей:
n^2 + n + 20(n^2 - 5n + 6) = 930
n^2 + n + 20n^2 - 100n + 120 = 930
21n^2 - 99n - 810 = 0
Сокращаем на 3:
7n^2 - 33n - 270 = 0
D = (-33)^2 - 4*7(-270) = 1089 + 7560 = 8649 = 93^2
Так как n ≥ 0, то подходит только один корень:
n = (33 + 93)/14 = 126/14 = 9