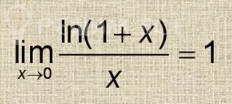Задача 75188 ...
Условие
{0, x=0 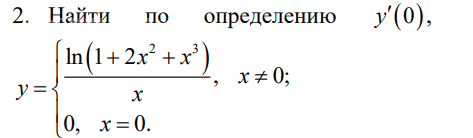
Решение
x_(o)+ Δx =0+ Δx
f(x_(o))=f(0)=0
f(x_(o)+ Δx)=f(0+ Δx)=[m]\frac{ln(1+2( Δx)^2+( Δx)^3)}{Δx}[/m]
Δf= f(0+ Δx)-f(0)=[m]\frac{ln(1+2( Δx)^2+( Δx)^3)}{0+Δx}-0=\frac{ln(1+2( Δx)^2+( Δx)^3)}{Δx}[/m]
[m]f`(0)=lim_{ Δx → 0}\frac{Δf}{ Δx}=lim_{ Δx → 0}\frac{\frac{ln(1+2( Δx)^2+( Δx)^3)}{Δx}}{ Δx}=lim_{ Δx → 0}\frac{ln(1+2( Δx)^2+( Δx)^3)}{(Δx)^2}=lim_{ Δx → 0}\frac{ln(1+2( Δx)^2+( Δx)^3)}{(1+2( Δx)^2+( Δx)^3)}\cdot \frac{(1+2( Δx)^2+( Δx)^3)}{(Δx)^2}=[/m]
[m]=lim_{ Δx → 0}\frac{ln(1+2( Δx)^2+( Δx)^3)}{(1+2( Δx)^2+( Δx)^3)}\cdot lim_{ Δx → 0}\frac{(1+2( Δx)^2+( Δx)^3)}{(Δx)^2}=1\cdot lim_{ t → 0}\frac{(1+2t^2+t^3)}{t^2}=1\cdot 2=2[/m]
применяем правило Лопиталя:
[m]lim_{ t → 0}\frac{(1+2t^2+t^3)}{t^2}=lim_{ t → 0}\frac{(4t+3t^2)}{2t}=lim_{ t → 0}\frac{4+6t}{2}=2[/m]