Задача 74975 на фото вариант 26. там 2 задания...
Условие

Решение
1. 1 функция. y = x + 1/x^2
План исследования функции:
1) Найти область определения функции.
x ≠ 0; x ∈ (-oo; 0) U (0; +oo)
В точке x = 0 - неустранимый разрыв 2 рода (уход в oo)
2) Исследовать функцию на чётность и периодичность.
Не четная и не нечетная, не периодическая.
3) Найти точки пересечения графика функции с осями координат.
Точка пересечения с осью Oy - отсутствует.
Точка пересечения с осью Ox:
x + 1/x^2 = 0
1/x^2 = -x
1 = -x^3
x = -1
Точка (-1; 0)
4) Найти интервалы знакопостоянства.
При x < -1 будет y < 0
При x ∈ (-1; 0) U (0; +oo) будет y > 0
5) Найти первую производную, промежутки возрастания и убывания, точки экстремума и экстремумы функции.
y' = 1 - 2x^(-3) = 1 - 2/x^3 = (x^3 - 2)/x^3
Экстремумы:
y' = 0
(x^3 - 2)/x^3 = 0
x^3 = 2
[m]x = \sqrt[3]{2}; y = x + \frac{1}{x^2} = \sqrt[3]{2} + \frac{1}{\sqrt[3]{4}}= \frac{\sqrt[3]{2} \cdot \sqrt[3]{4} + 1}{\sqrt[3]{4}} = \frac{\sqrt[3]{8}+ 1}{\sqrt[3]{4}} = \frac{3}{\sqrt[3]{4}}[/m]
Это точка минимума.
Точка минимума: [m](\sqrt[3]{2}; \frac{3}{\sqrt[3]{4}})[/m]
6) Найти вторую производную. Определить интервалы выпуклости графика функции и точки перегиба.
y'' = (1 - 2x^(-3))' = -2(-3)x^(-4) = 6x^(-4) = 6/x^4
6/x^4 > 0 при любом x ≠ 0, поэтому точек перегиба нет.
Функция всюду выпуклая вниз, то есть вогнутая.
7) Исследовать поведение функции на концах промежутков определения.
[m]\lim \limits_{x \to -\infty} (x + \frac{1}{x^2}) = -\infty + \frac{1}{+\infty} = -\infty[/m]
[m]\lim \limits_{x \to +\infty} (x + \frac{1}{x^2}) = +\infty + \frac{1}{+\infty} = +\infty[/m]
[m]\lim \limits_{x \to 0-0} (x + \frac{1}{x^2}) = 0 + \frac{1}{0+0} = +\infty[/m]
[m]\lim \limits_{x \to 0+0} (x + \frac{1}{x^2}) = 0 + \frac{1}{0+0} = +\infty[/m]
8) Найти асимптоты графика функции.
Вертикальная асимптота в точке разрыва: x = 0
Наклонные и горизонтальные асимптоты на бесконечности.
Асимптота на бесконечности имеет вид: f(x) = kx + b, где:
[m]k = \lim \limits_{x \to \infty} \frac{y(x)}{x} = \lim \limits_{x \to \infty} (1 + \frac{1}{x^3}) = 1 + \frac{1}{\infty} = 1 + 0 = 1[/m]
[m]b = \lim \limits_{x \to \infty} (y(x) - kx) = \lim \limits_{x \to \infty} (x + \frac{1}{x^2} - 1x) = \lim \limits_{x \to \infty} \frac{1}{x^2} = \frac{1}{\infty} = 0[/m]
Асимптота имеет вид:
f(x) = 1*x + 0
[b]f(x) = x[/b]
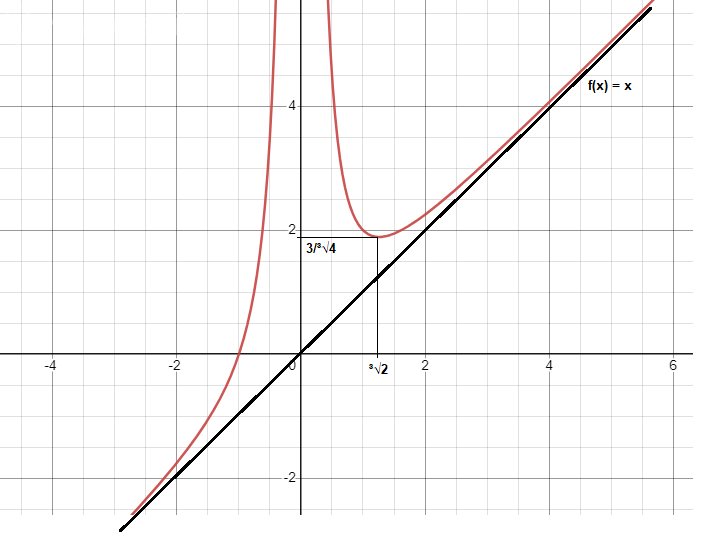
9) Построить график функции.
Прилагается. На графике показаны:
Точка минимума ([m](\sqrt[3]{2}; \frac{3}{\sqrt[3]{4}})[/m]) и
Асимптота [b]f(x) = x[/b]
Решу еще 2 задание.
y = ln(x^2) + 2/x; x ∈ [1/2; 2]
Найдем значения на концах отрезка.
y(1/2) = ln(1/4) + 2 : (1/2) = -ln(4) + 4 ≈ 2,614
y(2) = ln(4) + 2 : 2 = ln(4) + 1 ≈ 2,386
Найдем экстремумы.
[m]y' = \frac{1}{x^2} \cdot 2x - \frac{2}{x^2} = \frac{2}{x} - \frac{2}{x^2} = \frac{2x - 2}{x^2} = 0[/m]
x = 1
y(1) = ln(1^2) + 2/1 = 0 + 2 = 2 - точка минимума.
Наименьшее значение: y(1) = 2
Наибольшее значение: y(1/2) = 4 - ln(4)