Задача 74666 Найти точки пересечения поверхности и...
Условие
23 задача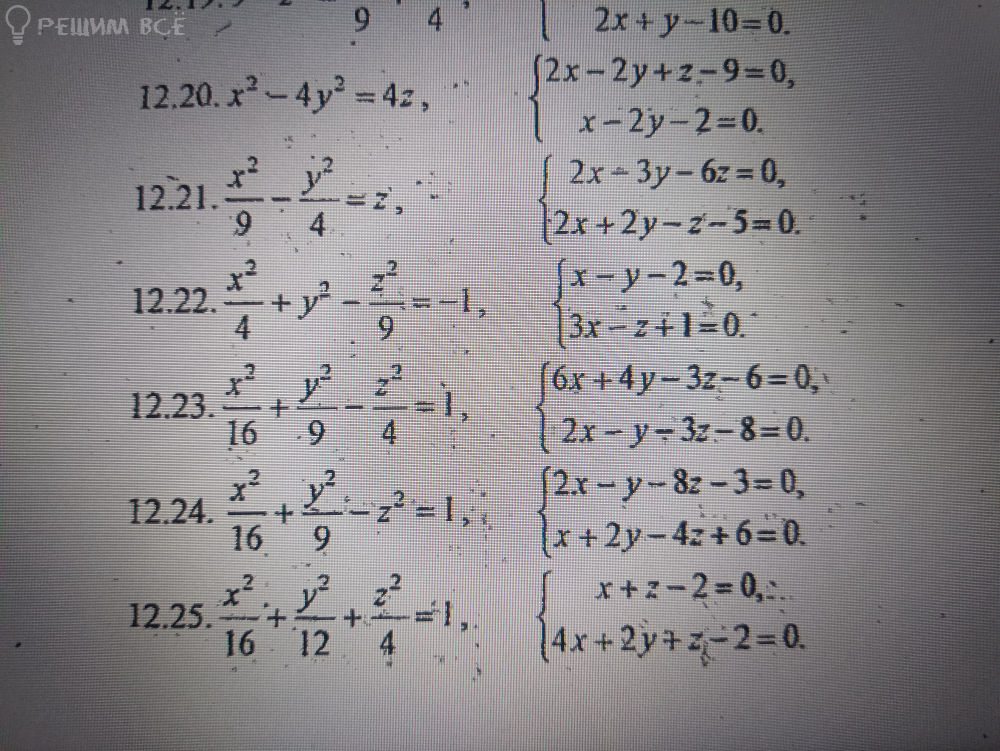
Решение
[m]\left\{\begin {matrix}\frac{x^2}{16}+\frac{y^2}{9}-\frac{z^2}{4}=1\\6x+4y-3z-6=0\\2x-y-3z-8=0\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}\frac{x^2}{16}+\frac{y^2}{9}=1+\frac{z^2}{4}=1\\3z=6x+4y-6\\3z=2x-y-8\end {matrix}\right.[/m]⇒ [m]\left\{\begin {matrix}9x^2+16y^2=144+36z^2\\3z=6x+4y-6\\6x+4y-6=2x-y-8\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}9x^2+16y^2=144+36z^2\\3z=6x+4y-6\\x=\frac{-5y-2}{4}\end {matrix}\right.[/m]⇒[m]\left\{\begin {matrix}9x^2+16y^2=144+36z^2\\3z=6\cdot \frac{-5y-2}{4}+4y-6\\x=\frac{-5y-2}{4}\end {matrix}\right.[/m]⇒[m]\left\{\begin {matrix}9x^2+16y^2=144+36z^2\\z= \frac{-30y-12+16y-24}{12}\\x=\frac{-5y-2}{4}\end {matrix}\right.[/m][m]\left\{\begin {matrix}9x^2+16y^2=144+36z^2\\z= \frac{-7y}{6}-3\\x=\frac{-5y-2}{4}\end {matrix}\right.[/m]
и подставляем в первое уравнение:
[m]9(\frac{-5y-2}{4})^2+16y^2=144+36(\frac{-7y}{6}-3)^2[/m]
[m]9(\frac{5y+2}{4})^2-36(\frac{+7y}{6}+3)^2=144-16 y^2[/m]
Применяем формулу разности квадратов:
[m](3(\frac{5y+2}{4})-6(\frac{+7y}{6}+3))(3(\frac{5y+2}{4})+6(\frac{+7y}{6}+3))=144-16 y^2[/m]
[m](\frac{15y+6}{4}-7y-18)(\frac{15y+6}{4}+7y+18)=144-16 y^2[/m]
[m]\frac{15y+6-28y-72}{4}\cdot \frac{15y+6+28y+72}{4}=144-16 y^2[/m]
[m](13y+66)(43y+78)=256y^2-144\cdot 16[/m]
[m]559y^2+2838y+1014y+5148=156y^2-2304[/m]
[m]303y^2+3852y+7452=0[/m]
[m]101y^2+1284y+2484=0[/m]
D/4=(642)^2-101*2484=161280=16^2*3^2*70
y_(1)=(-642-48sqrt(70))/101 или y_(2)=(-642+48sqrt(70))/101
Находим
x_(1) и x_(2)
z_(1) и z_(2)
Аналитический способ :
Прямая задана как линия пересечения двух плоскостей с нормальными векторами
vector{n_(1)}=(6;4;-3)
vector{n_(2)}=(2;-1;-3)
Составить параметрическое уравнение прямой:
vector{s}=vector{n_(1)} × vector{n_(2)}=[m]\begin {vmatrix} \vec{i}&\vec{j}&\vec{k}\\6&4&-3\\2&-1&-3\end {vmatrix}=-12\vec{i}-6\vec{j}-6\vec{k}-8\vec{k}-3\vec{i}+18\vec{j}=-15\vec{i}+12\vec{j}-14\vec{k}[/m]
vector{s}=(-15;12;-14)
И найдем точку M_(o)(x_(o);y_(o);z_(o)), принадлежащую прямой
Пусть y _(o)=0
Тогда система принимает вид:
[m]\left\{\begin {matrix}6x_{o}-3z_{o}-6=0\\2x_{o}-3z_{o}-8=0\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}3z_{o}=6x_{o}-6\\3z_{o}=2x_{o}-8\end {matrix}\right.[/m]
приравниваем правые части:
6x_(o)-6=2_(o)-8
x_(o)=-1/2
z_(o)=-3
Уравнение прямой:
[m]\frac{x+\frac{1}{2}}{-15}=\frac{y-0}{12}=\frac{z+3}{-14}[/m]
Параметризуем:
[m]\frac{x+\frac{1}{2}}{-15}=\frac{y-0}{12}=\frac{z+3}{-14}=t[/m] ⇒
[m]x+\frac{1}{2}=-15t[/m] ⇒ [m]x=-15t-\frac{1}{2}[/m]
[m]y=12t[/m] ⇒ [m]y=12t[/m]
[m]z+3=-14t[/m] ⇒ [m]z=-14t-3[/m]
Подставляем в уравнение поверхности:
[m]\frac{x^2}{16}+\frac{y^2}{9}-\frac{z^2}{4}=1[/m]
[m]\frac{(-15t-\frac{1}{2})^2}{16}+\frac{(12t)^2}{9}-\frac{(-14t-3)^2}{4}=1[/m]
Получим квадратное уравнение относительно t
[m]17t^2-321t+\frac{207}{4}=0[/m]
[m]D=321^2-4\cdot 17\cdot \frac{207}{4}=103 041 -3519=99522[/m]
Находим
t ( может быть не более двух значений)
и затем находим координаты точки
(подставляем найденные значения ):
t_(1)=
[m]x=-15t-\frac{1}{2}[/m]
[m]y=12t[/m]
[m]z=-14t-3[/m]
t_(2)=
[m]x=-15t-\frac{1}{2}[/m]
[m]y=12t[/m]
[m]z=-14t-3[/m]