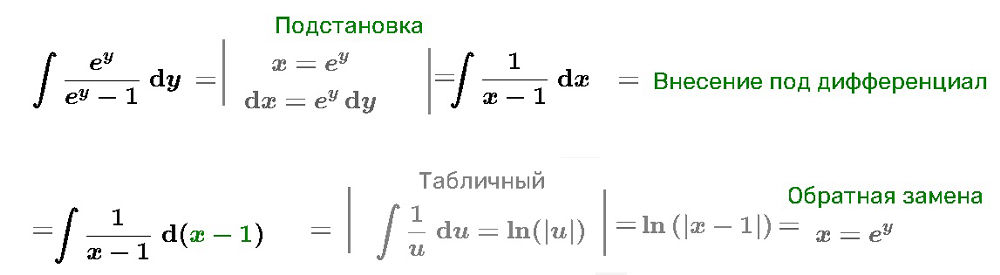Задача 74558 (16 вариант)Задание 1.Найти общее...
Условие
(16 вариант)Задание 2.Найти общее решение дифференциального уравнения и выделить частное решение, удовлетворяющее начальному условию
(16вариант)3 Задание Показать ,что данные дифференциальные уравнения являются однородными и решить их
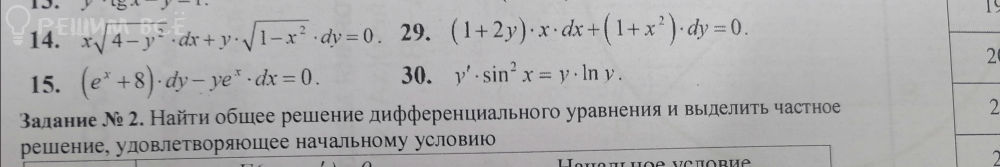


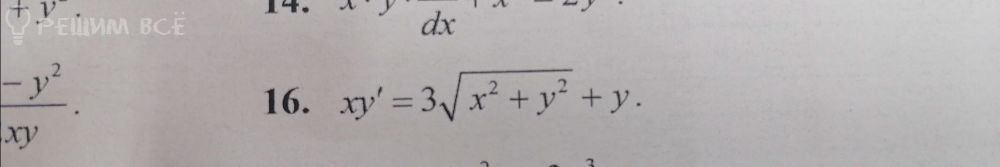
Решение
[m]e^{y}\cdot (1+\frac{dy}{dx})=1[/m]
[m]e^{y}\cdot (dx+dy)=dx[/m]
[m]e^{y}dx+e^{y}dy=dx[/m]
[m]e^{y}dx+e^{y}dy=dx[/m]
[m]e^{y}dx-dx=-e^{y}dy[/m] - уравнение с разделяющимися переменными
[m](e^{y}-1)dx=-e^{y}dy[/m] - уравнение с разделенными переменными
Интегрируем:
[m] ∫ dx=- ∫ \frac{e^{y}}{e^{y}-1}dy[/m]
[m]x=-ln|e^{y}-1| + C[/m]
( cм скрин 1)
[red][b]2.[/b][/red]
[m]2xyy`-1=0[/m]
[m]y`=\frac{dy}{dx}[/m]
[m]2xy\frac{dy}{dx}=1[/m]
[m]2ydy=\frac{1}{x}dx[/m] - уравнение с разделенными переменными
Интегрируем:
[m] ∫ 2ydy= ∫ \frac{1}{x}dx[/m]
[m]y^2=ln|x|+C[/m] - [i]общее решение
[/i]
[i]Частное решение[/i]
x_(o)=1
y_(o)=1
[m]1^2=ln|1|+C[/m] ⇒ [m]C=1[/m]
[m]y^2=ln|x|+1[/m] - [i] частное решение[/i], удовлетворяющее условию
x_(o)=1
y_(o)=1
[red][b]3.[/b][/red]
[m]xy`=3\sqrt{x^2+y^2}+y[/m]
[m]y`=\frac{3\sqrt{x^2+y^2}+y}{x}[/m]
Делим почленно каждое слагаемое на х:
[m]y`=\frac{3\sqrt{x^2+y^2}}{x}+\frac{y}{x}[/m]
Вносим х под корень:
[m]y`=\sqrt{3\frac{x^2+y^2}{x^2}}+\frac{y}{x}[/m]
Делим почленно под корнем:
[m]y`=3\sqrt{1+\frac{y^2}{x^2}}+\frac{y}{x}[/m]
[m]y`=3\sqrt{1+(\frac{y}{x})^2}+\frac{y}{x}[/m]- однородное уравнение вида [m]y`= φ (\frac{y}{x})[/m]
[i]Замена переменной:[/i]
[m]\frac{y}{x}=u[/m] ⇒ [m]y=u\cdot x[/m] ⇒ [m]y`=u`\cdot x+u\cdot x`[/m]
[m]x`=1[/m], так как х - независимая переменная
Подставляем в уравнение:
[m]y`=3\sqrt{1+\frac{y^2}{x^2}}+\frac{y}{x}[/m]
Получаем:
[m]u`\cdot x+u=3\sqrt{1+u^2}+u[/m]
[m]u`\cdot x=3\sqrt{1+u^2}[/m]- уравнение с разделяющимися переменными
[m]\frac{du}{dx}\cdot x=3\sqrt{1+u^2}[/m]
[m]\frac{du}{\sqrt{1+u^2}}=3\frac{dx}{x}[/m]
Интегрируем:
[m] ∫ \frac{du}{d\sqrt{1+u^2}}=3 ∫ \frac{dx}{x}[/m]
[m]ln|u+\sqrt{1+u^2}=3ln|x|+ lnC[/m]
[m]ln|u+\sqrt{1+u^2}|=ln Cx^3[/m] ⇒[m] u+\sqrt{1+u^2}=Cx^3[/m]
Обратная замена:
[m] \frac{y}{x}+\sqrt{1+(\frac{y}{x})^2}=Cx^3[/m]