Задача 73381 ...
Условие
x^(4)+ ∝ x^(3)+ β x^(2)+ γ x+ δ = 0
Как найти элементы множества В? Мой вариант 21 в таблице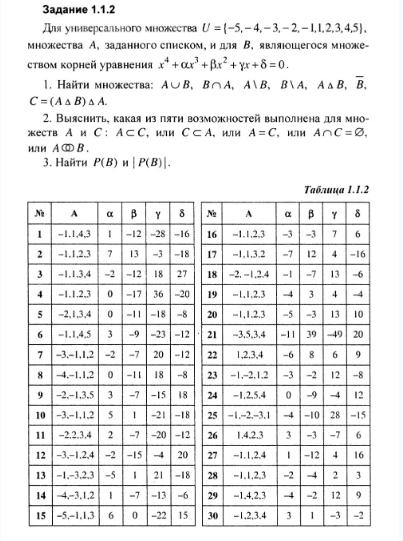
Решение
Уравнение: x^4 - 11x^3 + 39x^2 - 49x + 20 = 0
Если уравнение имеет рациональные корни, то их можно выразить:
x = b/a, здесь:
b - делитель свободного члена 20, а - делитель старшего члена 1.
Так как a = 1, то все предполагаемые корни - целые.
Делители свободного члена: ±1; ±2; ±4; ±5; ±10; ±20.
y = x^4 - 11x^3 + 39x^2 - 49x + 20
Проверяем:
y(1) = 1 - 11 + 39 - 49 + 20 = 0; x1 = 1, делим многочлен на (x-1):
y = x^4 - 11x^3 + 39x^2 - 49x + 20 = (x - 1)(x^3 - 10x^2 + 29x - 20) = 0
y1 = x^3 - 10x^2 + 29x - 20
Снова проверяем x = 1:
y1(1) = 1 - 10 + 29 - 20 = 0; x2 = x1 = 1; делим опять на (x-1):
y1 = x^3 - 10x^2 + 29x - 20 = (x - 1)(x^2 - 9x + 20) = 0
y2 = x^2 - 9x + 20 = (x - 4)(x - 5) = 0
x3 = 4; x4 = 5
Корень 1 повторяется, поэтому в множество B он входит один раз.
[b]B = {1; 4; 5}[/b]
Решаем задания:
U = {-5; -4; -3; -2; -1; 1; 2; 3; 4; 5}; A = {-3; 3; 4; 5}; B = {1; 4; 5}
1. A ∩ B = {4; 5}; A ∪ B = {-3; 1; 3; 4; 5}; A \ B = {-3; 3}; B \ A = {1}
A Δ B = {-3; 1; 3}; -B (не B) = {-5; -4; -3; -2; -1; 2; 3}
C = (A Δ B) Δ A = {-3; 1; 3} Δ {-3; 3; 4; 5} = {1; 4; 5}
2. A = {-3; 3; 4; 5}; C = {1; 4; 5}; A ∩ C = {4; 5}
3. P(B) - это булеан множества B, множество всех подмножеств B.
P(B) = { ∅; {1}; {4}; {5}; {1; 4}; {1; 5}; {4; 5}; {1; 4; 5}}
|P(B)| - я не нашел, что это такое и не знаю, как сделать.