Задача 72413 ...
Условие
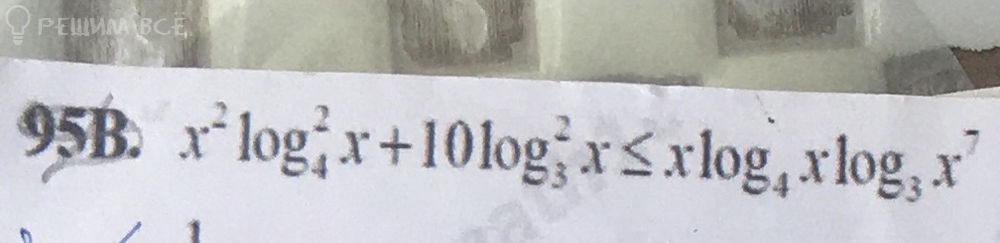
Решение

Все решения
Неравенство имеет смысл при
[b]x >0[/b]
По свойству логарифма степени
[m]x^2log^2_{4}x+10log^2_{3}x ≤ xlog_{4}x\cdot 7 \cdot log_{3}x[/m]
Замена переменной:
[m]log_{4}x=u[/m]
[m]log_{3}x=v[/m]
Неравенство принимает вид:
[m]x^2\cdot u^2+10\cdot v^2 ≤7\cdot x\cdot u\cdot v[/m]
Делим обе части уравнения на [m]v^2 ≠0 [/m]
[m]log^2_{3}x ≠0 [/m] ⇒ [m]x ≠1 [/m]
Получаем квадратное неравенство относительно [m]\frac{u}{v} [/m]
[m]x^2\cdot (\frac{u}{v})^2+10 ≤7\cdot x\cdot(\frac{u}{v})[/m]
[m]x^2\cdot (\frac{u}{v})^2-7\cdot x\cdot(\frac{u}{v})+10 ≤0 [/m]
[m]D=(7\cdot x)^2-4\cdot x^2\cdot 10=9x^2[/m]
[m]\frac{u}{v}=\frac{2}{x}[/m] или [m]\frac{u}{v}=\frac{5}{x}[/m]
Обратная замена
[m]\frac{log_{4}x}{log_{3}x}=\frac{2}{x}[/m] или [m]\frac{log_{4}x}{log_{3}x}=\frac{5}{x}[/m]
Применяем формулу перехода к другому основанию:
[m]\frac{\frac{log_{3}x}{log_{3}4}}{log_{3}x}=\frac{2}{x}[/m] или [m]\frac{\frac{log_{3}x}{log_{3}4}}{log_{3}x}=\frac{5}{x}[/m]
[m]\frac{1}{log_{3}4}=\frac{2}{x}[/m] или [m]\frac{1}{log_{3}4}=\frac{5}{x}[/m]
[m] log_{4}3=\frac{2}{x}[/m] или [m] log_{4}3=\frac{5}{x}[/m]
[m]x=2log_{3}4[/m] или [m] x=5log_{3}4[/m]
[m]x=2log_{3}2^2[/m] или [m] x=5log_{3}2^2[/m]
[m]x=4log_{3}2[/m] или [m] x=10log_{3}2[/m]
Решение неравенства
[m][4log_{3}2; 10log_{3}2][/m]
удовлетворяет условию x >0; x ≠ 1
[m]4log_{3}2=log_{3}2^4=log_{3}16 > log_{3}3=1[/m]
Проверим не является ли х=1 решением неравенства:
При х=1
[m]1^2\cdot log^2_{4}1+10\cdot log^2_{3}1 ≤ 1\cdot log_{4}1\cdot log_{3}1^7 [/m] - верно
О т в е т. [m]{1}\cup[4\cdot log_{3}2; 10\cdot log_{3}2][/m]