Задача 72394 Найти вторые частные производные...
Условие
функций. Убедиться в том, что ...
z = tg(x/y)
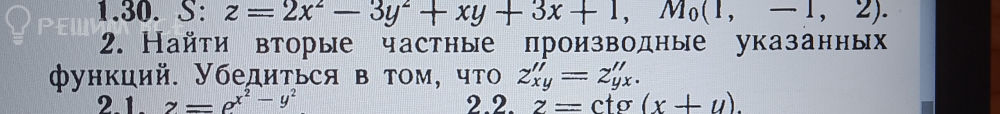
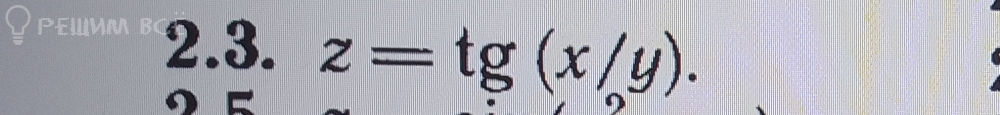
Решение
Производные 1 порядка:
[m]\frac{dz}{dx} = \frac{1}{cos^2(x/y)} \cdot \frac{1}{y} = \frac{1}{y} \cdot \frac{1}{cos^2(x/y)}[/m]
[m]\frac{dz}{dy} = \frac{1}{cos^2(x/y)} \cdot (-\frac{x}{y^2}) = -\frac{x}{y^2} \cdot \frac{1}{cos^2(x/y)}[/m]
Производные 2 порядка:
[m]\frac{d^2z}{dx^2} = (\frac{1}{y} \cdot \frac{1}{cos^2(x/y)})'_x = \frac{1}{y} \cdot \frac{-2}{cos^3(x/y)} \cdot (-sin(x/y)) \cdot \frac{1}{y} = \frac{2}{y^2} \cdot \frac{sin(x/y)}{cos^3(x/y)}[/m]
[m]\frac{d^2z}{dxdy} = (\frac{1}{y} \cdot \frac{1}{cos^2(x/y)})'_y = -\frac{1}{y^2} \cdot \frac{1}{cos^2(x/y)} + \frac{1}{y} \cdot \frac{-2}{cos^3(x/y)} \cdot (-sin(x/y)) \cdot \frac{-x}{y^2} = [/m]
[m]=-\frac{1}{y^2} \cdot \frac{1}{cos^2(x/y)} - \frac{2x}{y^3} \cdot \frac{sin(x/y)}{cos^3(x/y)} [/m]
[m]\frac{d^2z}{dydx} = (-\frac{x}{y^2} \cdot \frac{1}{cos^2(x/y)})'_x = -\frac{1}{y^2} \cdot \frac{1}{cos^2(x/y)} - \frac{x}{y^2} \cdot \frac{-2}{cos^3(x/y)} \cdot (-sin(x/y)) \cdot \frac{1}{y} = [/m]
[m]=-\frac{1}{y^2} \cdot \frac{1}{cos^2(x/y)} - \frac{2x}{y^3} \cdot \frac{sin(x/y)}{cos^3(x/y)} [/m]
Таким образом, мы доказали, что:
[m]\frac{d^2z}{dxdy} = \frac{d^2z}{dydx} = -\frac{1}{y^2} \cdot \frac{1}{cos^2(x/y)} - \frac{2x}{y^3} \cdot \frac{sin(x/y)}{cos^3(x/y)} [/m]
[m]\frac{d^2z}{dy^2} = (-\frac{x}{y^2} \cdot \frac{1}{cos^2(x/y)})'_y = -\frac{-2x}{y^3} \cdot \frac{1}{cos^2(x/y)} - \frac{x}{y^2} \cdot \frac{-2}{cos^3(x/y)} \cdot (-sin(x/y)) \cdot \frac{-x}{y^2} =[/m]
[m]= \frac{2x}{y^3} \cdot \frac{1}{cos^2(x/y)} + \frac{2x^2}{y^4} \cdot \frac{sin(x/y)}{cos^3(x/y)}[/m]