Задача 72307 Введите ответ без пробелов в виде...
Условие
Введите ответ без пробелов в виде числа. Если результат не является целым числом, то введите десятичную дробь (целую часть отделите точкой или запятой)
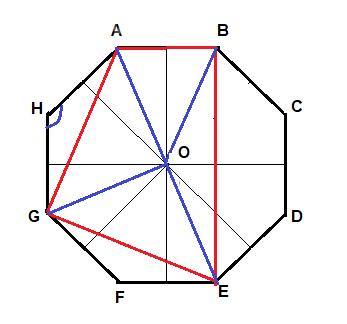
Найдите периметр правильного восьмнугольника ABCDEFGH, если площадь
четырехугольника ABEG 8(3 + 2корень2)
Решение
Обозначим сторону AB = BC = CD = ... = HA = a
Внутренний угол правильного 8-угольника:
ABC = BCD = CDE = ... = GHA = 180° - 360°/8 = 135°
Стороны AB = a; BE = 2a, AG = GE.
По теореме косинусов:
AG^2 = GE^2 = a^2 + a^2 - 2*a*a*cos 135° = 2a^2 - 2a^2*(-sqrt(2)/2) = a^2*(2 + sqrt(2))
AG = GE = a*sqrt(2 + sqrt(2))
Углы AOG = GOE = 90°, AOB = 45°; BOE = 135°
Значит, Δ AOG и Δ GOE - прямоугольные и равнобедренные.
А Δ AOB и Δ BOE - просто равнобедренные.
[m]OA = OB = OG = OE = \frac{AG}{\sqrt{2}} = \frac{a\sqrt{2+\sqrt{2}}}{\sqrt{2}}[/m]
Теперь нужно найти площадь 4-угольника ABEG как сумму четырех треугольников. Площади Δ AOB и Δ BOE ищем по формуле:
[m]S(AOB) = \frac{1}{2} \cdot OA \cdot OB \cdot \sin(AOB)[/m]
Заметим, что sin(45°) = sin(135°) = sqrt(2)/2
Поэтому их площади одинаковы:
[m]S(AOB) = \frac{1}{2} \cdot OA \cdot OB \cdot \sin(45°) = \frac{1}{2} \cdot \frac{a^2(2+\sqrt{2})}{2} \cdot \frac{\sqrt{2}}{2} = \frac{a^2(2\sqrt{2}+2)}{8} = \frac{a^2(\sqrt{2}+1)}{4}[/m]
[m]S(BOE) = \frac{1}{2} \cdot OB \cdot OE \cdot \sin(135°) = \frac{1}{2} \cdot \frac{a^2(2+\sqrt{2})}{2} \cdot \frac{\sqrt{2}}{2} = \frac{a^2(2\sqrt{2}+2)}{8} = \frac{a^2(\sqrt{2}+1)}{4}[/m]
Площади Δ AOG и Δ GOE ищем по другой формуле:
[m]S=\frac{OA \cdot OG}{2} = \frac{OA^2}{2}[/m]
Площадь прямоугольного треугольника равна половине произведения катетов. И они тоже одинаковы:
[m]S(AOG)=S(GOE)=\frac{OA^2}{2} = \frac{1}{2} \cdot \frac{a^2(2+\sqrt{2})}{2} = \frac{a^2(2+\sqrt{2})}{4}[/m]
Складываем эти площади:
[m]S(ABEG) = 2 \cdot \frac{a^2(\sqrt{2}+1)}{4} + 2 \cdot \frac{a^2(2+\sqrt{2})}{4} = \frac{a^2(\sqrt{2}+1)}{2} + \frac{a^2(2+\sqrt{2})}{2} =[/m]
[m] =\frac{a^2}{2} (\sqrt{2}+1 + 2+\sqrt{2}) = \frac{a^2}{2} (3+2\sqrt{2})[/m]
По условию
[m]S(ABEG) = 8(3+2\sqrt{2})[/m]
Отсюда:
[m]\frac{a^2}{2} (3+2\sqrt{2}) = 8(3+2\sqrt{2})[/m]
[m]a^2 = 16[/m]
[m]a = 4[/m]
Периметр 8-угольника:
[m]P=8a = 8 \cdot 4 = 32[/m]