Задача 72174 ...
Условие
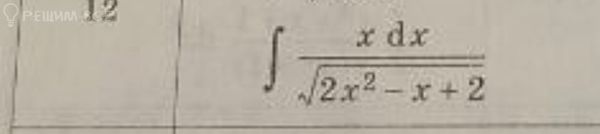
Решение
В 1 интеграле замена 2x^2 - x + 2 = t; dt = (4x - 1) dx
Во 2 интеграле выделяем квадрат в подкоренном выражении:
2x^2 - x + 2 = 2(x^2-1/2*x+1) = 2(x^2 - 2*1/4*x + (1/4)^2 - (1/4)^2 + 1) =
= 2((x - 1/4)^2 - 1/16 + 1) = 2((x - 1/4)^2 + 15/16)
[m]\int \frac{xdx}{\sqrt{2x^2-x+2}} = \frac{1}{4} (\int \frac{dt}{\sqrt{t}} + \frac{1}{\sqrt{2}} \int \frac{dx}{\sqrt{(x - 1/4)^2 + 15/16}}) =I[/m]
Оба интеграла - стандартные:
[m]\int \frac{dz}{\sqrt{z}} = 2\sqrt{z}[/m]
[m]\int \frac{dz}{\sqrt{z^2+a^2}} = \ln\ |z + \sqrt{z^2+a^2}|[/m] (так называемый длинный логарифм)
Получаем:
[m]I=\frac{1}{4} \cdot 2\sqrt{t} + \frac{1}{4} \cdot \frac{1}{\sqrt{2}} \cdot \ln\ |x - 1/4 + \sqrt{(x - 1/4)^2 + 15/16}| + C=[/m]
[m]= \frac{1}{2} \cdot \sqrt{2x^2-x+2} + \frac{1}{4\sqrt{2}} \cdot \ln\ |x - 1/4 + \sqrt{x^2-0,5x+1}| + C[/m]