Задача 71900 Задача на скрине...
Условие
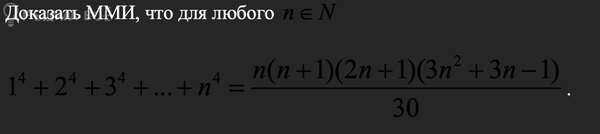
Решение
При n=1
[m]1^4=\frac{1\cdot (1+1)\cdot (2\cdot 1+1)\cdot (3\cdot 1^2+3\cdot 1-1)}{30}[/m] - верно, т. к[m]1=\frac{1\cdot 2\cdot 3\cdot 5}{30}[/m]
2)
Пусть равенство верно
для n=k
[m]1^4+2^4+3^4+...+k^4=\frac{k\cdot ( k+1)\cdot (2 k+1)\cdot (3k^2+3k-1)}{30}[/m]
3)
Докажем, используя предположение пункта 2). что верно и для n=k+1
[m]1^4+2^4+3^4+...+k^4+(k+1)^4=\frac{(k+1)\cdot ( (k+1)+1)\cdot (2\cdot( k+1)+1)\cdot (3\cdot( k+1)^2+3\cdot( k+1)-1)}{30}[/m]
[m]1^4+2^4+3^4+...+k^4+(k+1)^4=\frac{(k+1)\cdot ( k+2)\cdot (2 k+3)\cdot (3k^2+9 k+5)}{30}[/m]
Доказываем это тождество
Упрощаем левую часть:
[m]1^4+2^4+3^4+...+k^4+(k+1)^4=\frac{k\cdot ( k+1)\cdot (2 k+1)\cdot (3 k^2+3 k-1)}{30}+(k+1)^4=[/m]
[m]=\frac{(k+1)\cdot (k\cdot (2k+1)\cdot (3 k^2+3\cdot k-1)+30(k+1)^3)}{30}=\frac{(k+1)(6k^4+3k^3+6k^3+3k^2-2k^2-k+30k^3+90k^2+90k+30)}{30}=\frac{(k+1)(6k^4+39k^3+91k^2+89k+30)}{30}[/m]
Правая часть:
[m]\frac{(k+1)\cdot ( k+2)\cdot (2 k+3)\cdot (3k^2+9 k+5)}{30}=\frac{(k+1)(2k^2+7k+6)(3k^2+9 k+5)}{30}=\frac{(k+1)(6k^4+39k^3+91k^2+89k+30)}{30}[/m]
Левая часть равна правой части
Тождество 3) доказано
На основании принципа математической индукции ( аксиомы) равенство верно для любого натурального n