Задача 71881 С помощью двойного интеграла вычислить...
Условие
Решение
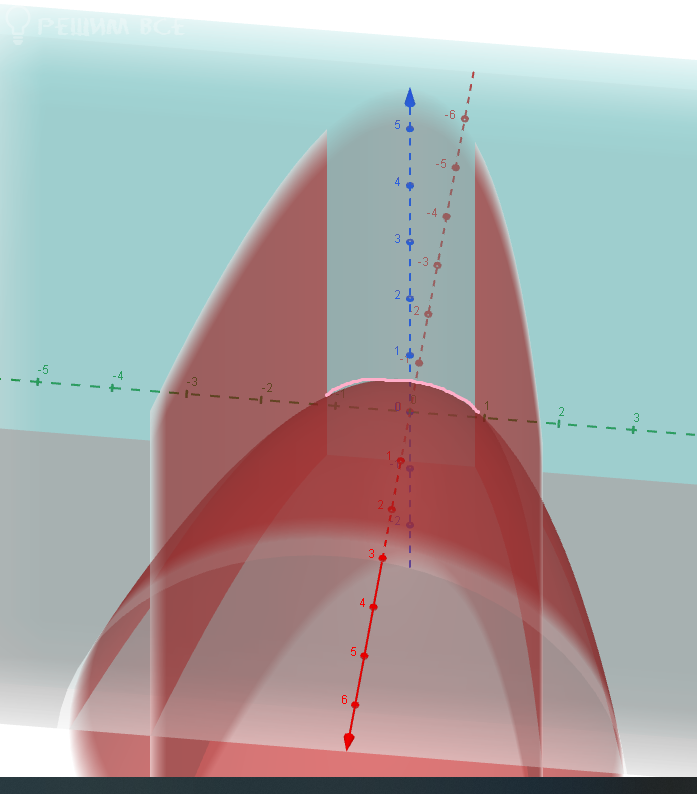
[m]y^2=ax[/m] - параболический цилиндр
[m]x=a[/m] плоскость, параллельна плоскости уОz
Поверхность проектируется на плоскость yOz
Применяем формулу
[m]S= ∫ ∫_{D_{yOz}}\sqrt{1+(\frac{ ∂ x}{ ∂y })^2+(\frac{ ∂ x}{ ∂z })^2}dydz[/m]
[m]\frac{ ∂ x}{ ∂y }=(\frac{1}{2a}(z^2+y^2))`_{y}=\frac{1}{2a}\cdot 2y=\frac{y}{a}[/m]
[m]\frac{ ∂ x}{ ∂z }=(\frac{1}{2a}(z^2+y^2))`_{z}=\frac{1}{2a}\cdot 2z=\frac{z}{a}[/m]
[m]S= ∫ ∫_{D_{yOz}}\sqrt{1+(\frac{y}{a})^2+(\frac{z}{a})^2}dydz=∫^{a}_{-a} dy( ∫^{\sqrt{2ax-y^2}} _{-\sqrt{2ax-y^2}}\frac{\sqrt{a^2+z^2+y^2}}{a}dz)=[/m]
переход к полярным координатам:
[m]y= ρ cos θ [/m]
[m]z= ρ sin θ [/m]
Тогда уравнение окружности
[m]z^2+y^2=2a[/m] в полярных координатах: [m] ρ ^2=2a[/m] ⇒ [m] ρ =\sqrt{2a}[/m]
уравнение прямой:
[m]y=a[/m] в полярных координатах: [m] ρcos θ =a[/m] ⇒ [m] ρ =\frac{a}{cos θ }[/m]
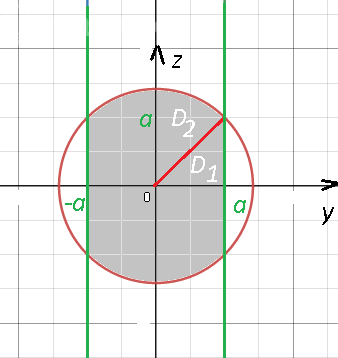
Область [m]D_{yOz}[/m] на рис. 4
Можно рассмотреть [m]\frac{1}{4}D_{yOz}=D_{1}+D_{2}[/m] в первой четверти
[m]D_{1} :0 ≤ θ ≤ \frac{π}{4}; 0 ≤ ρ ≤ \frac{a}{cos θ}[/m]
[m]D_{2} : \frac{π}{4}≤ θ ≤ \frac{π}{2}; 0 ≤ ρ ≤ \sqrt{2a}[/m]
[m]S= 4 \cdot ∫^{\frac{π}{4}}_{0}d θ ∫^{\frac{a}{cos θ}} _{0} \sqrt{a^2+ ρ^2} ρ d ρ )+ 4\cdot ∫^{\frac{π}{2}}_{\frac{π}{4}}d θ ∫^{\sqrt{2a}} _{0} \sqrt{a^2+ ρ^2} ρ d ρ )=4 \cdot ∫^{\frac{π}{4}}_{0}(∫^{\frac{a}{cos θ}} _{0}\frac{1}{2}(a^2+ ρ ^2)^{\frac{1}{2}}d(a^2+ ρ^2) d θ)+ 4\cdot ∫^{\frac{π}{2}}_{\frac{π}{4}} (∫^{\sqrt{2a}} _{0} \frac{1}{2}(a^2+ ρ^2)^{\frac{1}{2}}d(a^2+ ρ^2) d θ)=[/m]
По формуле [m] ∫ u^{\frac{1}{2}}du=\frac{ u^{\frac{1}{2}+1}}{\frac{1}{2}+1}[/m]