Задача 71848 ...
Условие
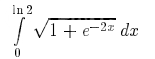
Решение
sqrt(1+e^(-2x)) = t
e^(-2x) = t^2 - 1
-2x = ln(t^2 - 1)
x = -0,5ln(t^2 - 1)
[m]dx = -0,5 \cdot \frac{2t}{t^2 - 1} dt= -\frac{t}{t^2 - 1} dt[/m]
Пределы интегрирования:
t(0) = sqrt(1+e^(0)) = sqrt(2)
t(ln 2) = sqrt(1+e^(-2ln 2)) = sqrt(1+1/e^(ln 4)) = sqrt(1+1/4) = sqrt(5/4) = sqrt(5)/2
Получаем интеграл:
[m]\int_{\sqrt{2}}^{\sqrt{5}/2} (-t \cdot \frac{t}{t^2-1})dt = -\int_{\sqrt{2}}^{\sqrt{5}/2} \frac{t^2}{t^2-1}dt = -\int_{\sqrt{2}}^{\sqrt{5}/2} (1 + \frac{1}{t^2-1})dt =[/m]
[m]=-(t -\frac{1}{2} ln|\frac{t+1}{t-1}| |_{\sqrt{2}}^{\sqrt{5}/2} =(\sqrt{2} - \frac{\sqrt{5}}{2}) + \frac{1}{2} \cdot (ln|\frac{\sqrt{5}+2}{\sqrt{5}-2}| - ln|\frac{\sqrt{2}+1}{\sqrt{2}-1}|)[/m]
Под логарифмами можно избавиться от иррациональности в знаменателе:
[m]\frac{\sqrt{5}+2}{\sqrt{5}-2} = \frac{(\sqrt{5}+2)^2}{(\sqrt{5}-2)(\sqrt{5}+2)} = \frac{(\sqrt{5}+2)^2}{5 - 4} = (\sqrt{5}+2)^2[/m]
[m]\frac{\sqrt{2}+1}{\sqrt{2}-1} = \frac{(\sqrt{2}+1)^2}{(\sqrt{2}-1)(\sqrt{2}+1)} =\frac{(\sqrt{2}+1)^2}{2-1} = (\sqrt{2}+1)^2[/m]
Получаем:
[m]\sqrt{2} - \frac{\sqrt{5}}{2} + \frac{1}{2} \cdot (ln|\frac{\sqrt{5}+2}{\sqrt{5}-2}| - ln|\frac{\sqrt{2}+1}{\sqrt{2}-1}|) = [/m]
[m] = \sqrt{2} - \frac{\sqrt{5}}{2} + \frac{1}{2} \cdot (ln|(\sqrt{5}+2)^2| - ln|(\sqrt{2}+1)^2|) =[/m]
[m]= \sqrt{2} - \frac{\sqrt{5}}{2} + \frac{1}{2} \cdot (2ln(\sqrt{5}+2) - 2ln(\sqrt{2}+1)) = [/m]
[m] = \sqrt{2} - \frac{\sqrt{5}}{2} + ln(\sqrt{5}+2) - ln(\sqrt{2}+1) = \sqrt{2} - \frac{\sqrt{5}}{2} + ln (\frac{\sqrt{5}+2}{\sqrt{2}+1})[/m]