Задача 71827 Исследовать на абсолютное и условное...
Условие
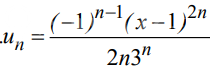
Решение
[m]a(n) = \frac{(x-1)^{2n}}{2n \cdot 3^{n}}[/m]
Рассмотрим предел:
[m]\lim \limits_{n \to \infty} \frac{a(n+1)}{a(n)} = \lim \limits_{n \to \infty} \frac{(x-1)^{2n+2}}{(2n+2) \cdot 3^{n+1}} : \frac{(x-1)^{2n}}{2n \cdot 3^{n}} = \lim \limits_{n \to \infty} \frac{(x-1)^{2n+2}}{(2n+2) \cdot 3^{n+1}} \cdot \frac{2n \cdot 3^{n}}{(x-1)^{2n}} =[/m]
[m]=\lim \limits_{n \to \infty} \frac{(x-1)^{2n} \cdot (x-1)^2}{(x-1)^{2n}} \cdot \frac{2n \cdot 3^{n}}{(2n+2) \cdot 3 \cdot 3^{n}} = \lim \limits_{n \to \infty} (x-1)^2 \cdot \frac{2n}{3(2n+2)} = [/m]
[m] =(x-1)^2 \cdot \lim \limits_{n \to \infty} \frac{n}{3n+3} = \frac{(x-1)^2}{3}[/m]
По признаку Даламбера, если
[m]\lim \limits_{n \to \infty} \frac{a(n+1)}{a(n)} < 1[/m]
То ряд сходится
[m]\frac{(x-1)^2}{3} < 1[/m]
(x - 1)^2 < 3
x^2 - 2x + 1 - 3 < 0
x^2 - 2x - 2 < 0
D= (-2)^2 - 4*1(-2) = 4 + 8 = 12 = (2sqrt(3))^2
x1 = (2 - 2sqrt(3))/2 = 1 - sqrt(3)
x2 = (2 + 2sqrt(3))/2 = 1 + sqrt(3)
На промежутке (1 - sqrt(3); 1 + sqrt(3)) ряд из модулей сходится.
Значит, знакопеременный ряд сходится абсолютно.