Задача 71327 Решить данные дифференциальные...
Условие
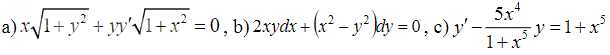
Решение
Уравнение 1 порядка с разделяющимися переменными.
[m]yy' \sqrt{1+x^2} = -x \sqrt{1+y^2}[/m]
[m]\frac{dy}{dx} \cdot \frac{y}{\sqrt{1+y^2}} = -\frac{x}{\sqrt{1+x^2}}[/m]
[m]\frac{ydy}{\sqrt{1+y^2}} = -\frac{xdx}{\sqrt{1+x^2}}[/m]
Берем интегралы от левой и правой части. Они одинаковые:
[m]\int \frac{ydy}{\sqrt{1+y^2}}[/m]
Решается заменой: t = 1 + y^2; dt = 2y dy
[m]\int \frac{ydy}{\sqrt{1+y^2}} = \int \frac{dt}{2\sqrt{t}} = \sqrt{t} = \sqrt{1+y^2}[/m]
Получаем:
[m]\sqrt{1+y^2} = -\sqrt{1+x^2} + C[/m]
b) 2xy dx + (x^2 - y^2) dy = 0
(y^2 - x^2)dy = 2xy dx
(y^2 - x^2)y' = 2xy
[m]y' = \frac{2xy}{y^2 - x^2}[/m]
Это однородное уравнение 1 порядка, решается заменой:
t = y/x; y = tx; y' = t'*x + t
[m]t' \cdot x + t = \frac{2xtx}{t^2x^2 - x^2}[/m]
Правую часть сокращаем на x^2:
[m]t' \cdot x + t = \frac{2t}{t^2 - 1}[/m]
[m]t' \cdot x = \frac{2t}{t^2 - 1} - t[/m]
[m]\frac{dt}{dx} \cdot x = \frac{2t - t^3 + t}{t^2 - 1}[/m]
Уравнение с разделяющимися переменными:
[m]\frac{t^2 - 1}{3t - t^3} dt = \frac{dx}{x}[/m]
Берем интегралы от левой и правой части.
В правой части все ясно, интеграл равен ln |x| + ln(C) = ln|Cx|
В левой части интеграл берется заменой:
3t - t^3 = z; dz = (3 - 3t^2) dt = 3(1 - t^2) dt; (t^2 - 1)dt = -1/3*dz
[m]\int \frac{t^2 - 1}{3t - t^3} dt = -\frac{1}{3} \int \frac{dz}{z} = -\frac{1}{3} ln |z| = -\frac{1}{3} ln |3t - t^3| = ln |\frac{1}{\sqrt[3]{3t - t^3}}|[/m]
Получаем:
[m]ln |\frac{1}{\sqrt[3]{3t - t^3}}| = ln|Cx|[/m]
[m]\frac{1}{\sqrt[3]{3t - t^3}} = Cx[/m]
Возвращаемся к функции y:
[m]\frac{1}{\sqrt[3]{3y/x - (y/x)^3}} = Cx[/m]
c) [m]y' - \frac{5x^4}{1+x^5} \cdot y = 1 + x^5[/m]
Это неоднородное уравнение 1 порядка, решается заменой:
y = u*v; y' = u'*v + u*v'
[m]u'v + uv' - \frac{5x^4}{1+x^5} \cdot uv = 1 + x^5[/m]
Выносим за скобки u:
[m]u'v + u(v' - \frac{5x^4}{1+x^5} \cdot v) = 1 + x^5[/m]
Скобку приравниваем к 0:
[m]v' - \frac{5x^4}{1+x^5} \cdot v = 0[/m]
Уравнение с разделяющимися переменными:
[m]\frac{dv}{dx} = \frac{5x^4}{1+x^5} \cdot v[/m]
[m]\frac{dv}{v} = \frac{5x^4\ dx}{1+x^5}[/m]
Берем интегралы от левой и правой части.
В левой части все ясно, интеграл равен ln |v|
В правой части интеграл берется заменой:
1 + x^5 = t; dt = 5x^4 dx
[m]\int \frac{5x^4\ dx}{1+x^5} = \int \frac{dt}{t} = ln |t| = ln |1+x^5|[/m]
Получаем:
ln |v| = ln |1+x^5|
v = 1+x^5
Подставляем в наше уравнение:
[m]u'v + u(v' - \frac{5x^4}{1+x^5} \cdot v) = 1 + x^5[/m]
[m]u'(1+x^5) + u \cdot 0 = 1 + x^5[/m]
Ну это просто подарок!
[m]u'(1+x^5) = 1 + x^5[/m]
u' = 1
u = x + C
Возвращаемся к функции y:
y = u*v = (x + C)(1 + x^5)