Задача 71206 Решить дифференциальное уравнение и...
Условие
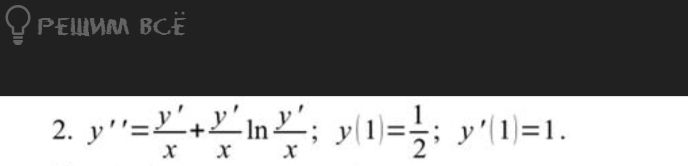
Решение
Т.е решается методом замены
[m]y`=z(x;y)[/m]
[m]y``=z`_{y}(x;y)[/m]
Уравнение принимает вид:
[m]z`=\frac{z}{x}+\frac{z}{x}ln\frac{z}{x}[/m]
[m]z`=\frac{dz}{dx}[/m]
[m]\frac{dz}{dx}=\frac{z}{x}+\frac{z}{x}ln\frac{z}{x}[/m]
[m]dz=(\frac{z}{x}+\frac{z}{x}ln\frac{z}{x})dx[/m] - однородное дифференциальное уравнение первого порядка.
Замена
[m]\frac{z}{x}=u[/m] ⇒ [m]z=u\cdot x[/m]
тогда
[m]dz=udx+xdu[/m]
Уравнение принимает вид:
[m]udx+xdu=(u+ulnu)dx[/m]
[m]udx+xdu=udx+ulnudx[/m]
[m]xdu=ulnudx[/m] - уравнение с разделяющимися переменными
[m]\frac{du}{ulnu}=\frac{dx}{x}[/m]
[m] ∫ \frac{du}{ulnu}= ∫ \frac{dx}{x}[/m]
[m]ln|lnu|=ln|x|+lnC_{1}[/m]
⇒
[m]ln|lnu|=lnC_{1}|x|[/m]
[m]lnu=C_{1}x[/m]
Обратный переход к переменной z:
[m]ln\frac{z}{x}=C_{1}x[/m]
[m]\frac{z}{x}=e^{C_{1}x}[/m]
Переход к переменной y:
[m]\frac{y`}{x}=e^{C_{1}x}[/m]
[m]y`=x\cdot e^{C_{1}x}[/m]
Интегрируем
[m]y= ∫ x\cdot e^{C_{1}x}dx[/m]
Интегрируем по частям
[m]u=x[/m]
[m]dv= e^{C_{1}x}dx[/m]
⇒
[m]du=dx[/m]
[m]v= ∫ e^{C_{1}x}dx=\frac{1}{C_{1}}e^{C_{1}x}[/m]
[m]y= ∫ x\cdot e^{C_{1}x}dx=\frac{x}{C_{1}}e^{C_{1}x}- ∫ \frac{1}{C_{1}}e^{C_{1}x}dx=\frac{x}{C_{1}}e^{C_{1}x}- \frac{1}{C^2_{1}}e^{C_{1}x}+C_{2}[/m]
Общее решение уравнения
[m]y= \frac{x}{C_{1}}e^{C_{1}x}- \frac{1}{C^2_{1}}e^{C_{1}x}+C_{2}[/m]
Решаем задачу с начальными условиями ( задача Коши)
[m]y(1)=\frac{1}{2}[/m]
[m]y(1)= \frac{1}{C_{1}}e^{C_{1}}- \frac{1}{C^2_{1}}e^{C_{1}}+C_{2}[/m]
[m]\frac{1}{2}= \frac{1}{C_{1}}e^{C_{1}}- \frac{1}{C^2_{1}}e^{C_{1}}+C_{2}[/m] ( умножим на С^2_(1))
C^2_{1}\frac{1}{2}= C_{1}e^{C_{1}}-e^{C_{1}}+C^2_{1}C_{2}\\1=1\cdot e^{C_{1}}
[m]y`(1)=1[/m]
[m]y`(1)=1\cdot e^{C_{1}}[/m]
[m]1=1\cdot e^{C_{1}}[/m]
Решаем систему двух уравнений и находим C_(1) и C_(2)
[m]\left\{\begin {matrix}C^2_{1}\frac{1}{2}= C_{1}e^{C_{1}}-e^{C_{1}}+C^2_{1}C_{2}\\1=1\cdot e^{C_{1}}\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}0=0-e^{0}+0\cdot C_{2}\\e^{0}=e^{C_{1}} ⇒C_{1}=0 \end {matrix}\right.[/m]
первое уравнение не имеет решений
0=-1
Значит нет частного решения.
Задача Коши не имеет решения.