Задача 71026 ...
Условие
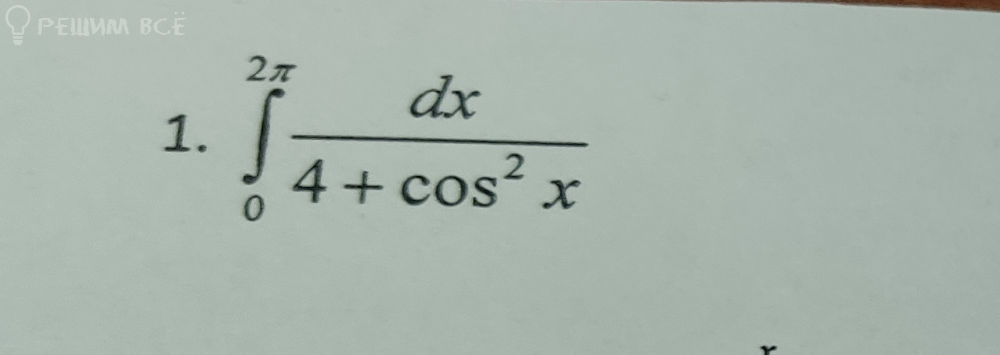
Решение
[m]tgx=t[/m] [red](tgx не является непрерывной на [0;2π])[/red] и имеет две точки разрыва [m] x=\frac{π}{2}[/m] и [m] x=\frac{3π}{2}[/m]
Значит рассматриваем определенный интеграл на трех промежутках ( см. ниже)
По формуле
[m]1+tg^2x=\frac{1}{cos^2x}[/m]
⇒ [m]cos^2x=\frac{1}{1+tg^2x}[/m]
[m]x=arctgt[/m]
[m]dx=\frac{1}{1+t^2}dt[/m]
Находим первообразную, вычисляем неопределенный интеграл
[m] ∫ \frac{dx}{4+cos^2x}= ∫ \frac{1}{4+\frac{1}{1+t^2}}\cdot \frac{1}{1+t^2}dt= ∫\frac{1}{4t^2+5}dt=\frac{1}{4}∫\frac{1}{t^2+\frac{5}{4}}dt\frac{1}{4\cdot \frac{\sqrt{5}}{2}}arctg \frac{t}{\frac{\sqrt{5}}{2}}+C=\frac{1}{2\sqrt{5}}arctg \frac{2tgx}{\sqrt{5}}+C [/m]
По формуле Ньютона Лейбница
[m] ∫^{b} _{a}f(x)dx=F(x)|^{b}_{a}=F(b)-F(a)[/m]
[m] ∫^{2π}_{0} \frac{1}{4+cos^2x}dx=∫^{\frac{π}{2}-0}_{0} \frac{1}{4+cos^2x}dx+∫^{\frac{3π}{2}-0}_{\frac{π}{2}+0} \frac{1}{4+cos^2x}dx+∫^{2π}_{\frac{3π}{2}+0} \frac{1}{4+cos^2x}dx=[/m]
[m]=(\frac{1}{2\sqrt{5}}arctg \frac{2tgx}{\sqrt{5}})|^{\frac{π}{2}-0}_{0}+(\frac{1}{2\sqrt{5}}arctg \frac{2tgx}{\sqrt{5}})|^{\frac{3π}{2}-0}_{\frac{π}{2}+0}+(\frac{1}{2\sqrt{5}}arctg \frac{2tgx}{\sqrt{5}})|^{2π}_{\frac{3π}{2}+0}=[/m]
[m]=(\frac{1}{2\sqrt{5}}\cdot arctg (+∞ )- \frac{1}{2\sqrt{5}}\cdot arctg 0)+(\frac{1}{2\sqrt{5}}\cdot arctg (+∞ )- \frac{1}{2\sqrt{5}}\cdot arctg (- ∞ )+(\frac{1}{2\sqrt{5}}\cdot arctg (+∞ )- \frac{1}{2\sqrt{5}}\cdot arctg 0)=[/m]
[m]=(\frac{1}{2\sqrt{5}}\cdot \frac{π}{2}-\frac{1}{2\sqrt{5}}\cdot 0+(\frac{1}{2\sqrt{5}}\cdot \frac{π}{2}- \frac{1}{2\sqrt{5}}\cdot (-\frac{π}{2})+(\frac{1}{2\sqrt{5}}\cdot \frac{π}{2}- \frac{1}{2\sqrt{5}}\cdot 0)=\frac{π}{\sqrt{5}}[/m]