Задача 70961 Определить тип дифференциального...
Условие
Если возможно, то подобрать замену, соответствующую типу уравнения. Замена упростит решение, появится возможность свести исходное уравнение к уравнению с разделяющимися переменными.
Не забудьте вернуться к исходным переменным.
Помните: в результате интегрирования дифференциального уравнения должно получиться семейство функций, зависящих от одной произвольной постоянной С.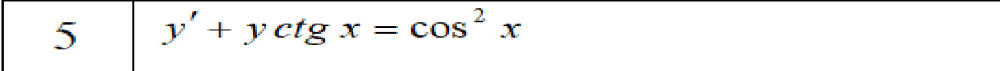
Решение
Это неоднородное уравнение 1 порядка.
Решается заменой y = u*v; тогда y' = u'*v + u*v'
u'*v + u*v' + u*v*ctg x = cos^2 x
Выносим u за скобки
u'*v + u*(v' + v*ctg x) = cos^2 x
Скобку приравниваем к 0
v' + v*ctg x = 0
v' = -v*ctg x
dv/dx = -v*ctg x
Это уравнение с разделяющимися переменными.
dv/v = -ctg x dx
Берем интегралы от обеих частей.
[m]\int \frac{dv}{v} = ln|v|[/m]
[m]\int (-ctg(x)dx) = -\int \frac{cos(x)}{sin(x)} dx[/m]
Этот интеграл решается заменой t = sin x; dt = cos x dx
[m]-\int \frac{cos(x)}{sin(x)} dx = -\int \frac{dt}{t} = -ln|t| = -ln|sin x| = ln|\frac{1}{sin x}|[/m]
Подставляем:
ln |v| = ln |1/sin x|
v = 1/sin x
Подставляем v в исходное уравнение:
u'*1/sin x + u*0 = cos^2 x
u' = sin x*cos^2 x
Этот интеграл берется заменой t = cos x; dt = -sin x dx
[m]u = \int sin(x)cos^2(x) dx = -\int t^2 dt = -\frac{t^3}{3} + C = -\frac{cos^3(x)}{3} + C[/m]
Возвращаемся к функции y = u*v:
[m]y = u \cdot v = (-\frac{cos^3(x)}{3} + C) \cdot \frac{1}{sin(x)} = -\frac{cos^3(x)}{3sin(x)} + \frac{C}{sin(x)}[/m]