Задача 70943 ...
Условие
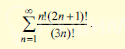
Решение
По признаку Даламбера найдем предел:
[m]\lim \limits_{n \to \infty} \frac{a_{n+1}}{a_{n}} = \lim \limits_{n \to \infty} \frac{(n+1)!(2n+3)!}{(3n+3)!} : \frac{n!(2n+1)!}{(3n)!} =[/m]
[m]=\lim \limits_{n \to \infty} \frac{(n+1)!}{n!} \cdot \frac{(2n+3)!}{(2n+1)!} \cdot \frac{(3n)!}{(3n+3)!} = [/m]
[m]=\lim \limits_{n \to \infty} \frac{n!(n+1)}{n!} \cdot \frac{(2n+1)!(2n+2)(2n+3)}{(2n+1)!} \cdot \frac{(3n)!}{(3n)!(3n+1)(3n+2)(3n+3)} =[/m]
[m]=\lim \limits_{n \to \infty} (n+1) \cdot (2n+2)(2n+3) \cdot \frac{1}{(3n+1)(3n+2)(3n+3)} =[/m]
[m]=\lim \limits_{n \to \infty} \frac{(n+1)(4n^2+4n+6n+6)}{(3n+1)(9n^2+6n+9n+6)} =\lim \limits_{n \to \infty} \frac{(n+1)(4n^2+10n+6)}{(3n+1)(9n^2+15n+6)}=[/m]
[m]=\lim \limits_{n \to \infty} \frac{4n^3+10n^2+6n+4n^2+10n+6}{27n^3+45n^2+18n+9n^2+15n+6} = \lim \limits_{n \to \infty}\frac{4n^3+14n^2+16n+6}{27n^3+54n^2+33n+6} = \frac{4}{27} < 1[/m]
Так как [m]\lim \limits_{n \to \infty} \frac{a_{n+1}}{a_{n}} < 1[/m]
То по признаку Даламбера ряд сходится.