Задача 70923 ...
Условие
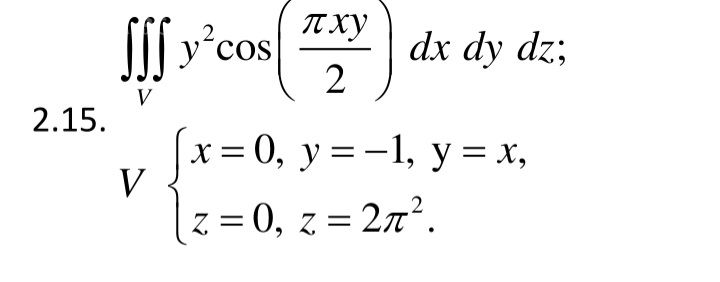
Решение
-1<y < 0
y<x<0
0 < z < 2π^2
[m] ∫ ∫ ∫_{ Ω }y^2cos\frac{πxy}{2}dxdydz= ∫ ^{2π^2}_{0}dz ∫^{0} _{-1}y^2dy ∫^{0} _{y}cos\frac{πxy}{2}dx=[/m]
[m]=y^2 ∫^{0} _{y}cos\frac{πxy}{2}dx=[/m]
Замена переменной:
[m]\frac{πxy}{2}=u[/m]
(y =cosnst(!) ⇒
[m]x=\frac{2}{πy}u[/m]
[m]dx=\frac{2}{πy}du[/m]
Пределы интегрирования
[m] x=0[/m] ⇒ [m]u=0[/m]
[m] x=y[/m] ⇒ [m]u=\frac{πy^2}{2}[/m]
[m] y^2∫^{0} _{y}cos\frac{πxy}{2}dx= y^2∫^{\frac{πy^2}{2}}_{0} cosu \cdot ( \frac{2}{πy} du )=y^2\cdot \frac{2}{πy} (sinu)|^{\frac{πy^2}{2}}_{0}=\frac{2y}{π}\cdot sin\frac{πy^2}{2}[/m]
[m] ∫ ∫ ∫_{ Ω }cos\frac{πxy}{2}dxdydz= ∫ ^{2π^2}_{0}dz ∫^{0} _{-1}y^2dy ∫^{0} _{y}cos\frac{πxy}{2}dx= ∫ ^{2π^2}_{0}dz ∫^{0} _{-1}\frac{2y}{π}(sin\frac{πy^2}{2})dy=∫ ^{2π^2}_{0}dz\frac{2}{π}∫^{0} _{-1}y\cdot sin\frac{πy^2}{2})dy[/m]
замена переменной:
[m]\frac{πy^2}{2}=u[/m]
⇒
[m]u=\frac{2}{π}y^2[/m]
[m]du=\frac{2}{π}\cdot 2ydy[/m]
[m]ydy=\frac{π}{4}\cdot du[/m]
Пределы интегрирования
[m] y=0[/m] ⇒ [m]u=0[/m]
[m] y=-1[/m] ⇒ [m]u=\frac{2}{π}[/m]
[m] ∫ ∫ ∫_{ Ω }cos\frac{πxy}{2}dxdydz= ∫ ^{2π^2}_{0}dz ∫^{0} _{-1}y^2dy ∫^{0} _{y}cos\frac{πxy}{2}dx= ∫ ^{2π^2}_{0}dz ∫^{0} _{-1}\frac{2y}{π}(sin\frac{πy^2}{2})dy=[/m]
[m]=∫ ^{2π^2}_{0}dz(\frac{2}{π})∫^{0} _{-1}y\cdot sin\frac{πy^2}{2})dy=\frac{2}{π}\cdot ∫ ^{2π^2}_{0}dz∫^{\frac{2}{π}} _{0}\cdot sinu (\frac{π}{4}\cdot du)=\frac{1}{2}∫ ^{2π^2}_{0}dz(∫^{\frac{2}{π}} _{0} sinudu)=\frac{1}{2}∫ ^{2π^2}_{0}(sin\frac{2}{π}-sin0)dz=\frac{1}{2}sin\frac{2}{π} (z)|^{2π^2}_{0}=π^2\cdot sin\frac{2}{π}[/m]
Вот теперь вроде все верно