Задача 70823 Найти радиус и интервал сходимости...
Условие
точках интервала сходимости: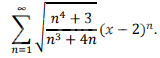
Решение
[m]a_{n} = \sqrt{\frac{n^4+3}{n^3+4n}}(x-2)^{n}[/m]
По признаку Даламбера рассмотрим предел:
[m]\lim \limits_{n \to \infty} \frac{a_{n+1}}{a_{n}}=\lim \limits_{n \to \infty} \sqrt{\frac{(n+1)^4+3}{(n+1)^3+4(n+1)}}(x-2)^{n+1} : \sqrt{\frac{n^4+3}{n^3+4n}}(x-2)^{n} =[/m]
[m]= \lim \limits_{n \to \infty} \sqrt{\frac{((n+1)^4+3)(n^3+4n)}{((n+1)^3+4n+4)(n^4+3)}} \cdot \frac{(x-2)^{n+1}}{(x-2)^{n}}[/m]
Если этот предел < 1, то ряд сходится, а если > 1, то расходится.
[m]\lim \limits_{n \to \infty} \sqrt{\frac{(n^4+4n^3+6n^2+4n+1+3)(n^3+4n)}{(n^3+3n^2+3n+1+4n+4)(n^4+3)}} \cdot (x-2) =[/m]
[m]\lim \limits_{n \to \infty} \sqrt{\frac{(n^4+4n^3+6n^2+4n+4)(n^3+4n)}{(n^3+3n^2+7n+5)(n^4+3)}} \cdot (x-2) =[/m]
[m]\lim \limits_{n \to \infty} \sqrt{\frac{n^7 + 4n^6 + 6n^5 + 4n^4 + 4n^3+4n^5+16n^4+24n^3+16n^2+16n}{n^7 + 3n^6 + 7n^5 + 5n^4 + 3n^3+9n^2+21n+15}} \cdot (x-2) =[/m]
[m]\lim \limits_{n \to \infty} \sqrt{\frac{n^7 + 4n^6 + 10n^5 + 20n^4 + 28n^3+16n^2+16n}{n^7 + 3n^6 + 7n^5 + 5n^4 + 3n^3+9n^2+21n+15}} \cdot (x-2)[/m]
В дроби делим числитель и знаменатель на старший член n^7.
[m]\lim \limits_{n \to \infty} \sqrt{\frac{1 + 4/n + 10/n^2 + 20/n^3 + 28/n^4+16/n^5+16/n^6}{1 + 3/n + 7/n^2 + 5/n^3 + 3/n^4+9/n^5+21/n^6+15/n^7}} \cdot (x-2) =[/m]
[m]= \sqrt{\frac{1 + 0 + 0 + 0 + 0+0+0}{1 + 0 + 0 + 0 + 0 +0 +0 +0}} \cdot (x-2) =1\cdot (x-2) = x-2 < 1[/m]
Получили:
|x - 2| < 1
-1 < x - 2 < 1
[b]1 < x < 3[/b]
Радиус сходимости [b]R = 1[/b]
Интервал сходимости: [b]x ∈ (1; 3)[/b]
В конечных точках:
При x = 1 будет ряд:
[m]a_{n} = \sqrt{\frac{n^4+3}{n^3+4n}}(1-2)^{n} = (-1)^n\sqrt{\frac{n^4+3}{n^3+4n}}[/m]
Это знакопеременный ряд, он расх., потому что ряд из модулей расх.:
[m]\lim \limits_{n \to \infty} \sqrt{\frac{n^4+3}{n^3+4n}} = \lim \limits_{n \to \infty} \sqrt{\frac{1+3/n^4}{1/n+4/n^3}} = \sqrt{\frac{1+0}{0+0}} = \infty[/m]
n-ный член постоянно растет и стремится к бесконечности.
При x = 3 будет ряд:
[m]a_{n} = \sqrt{\frac{n^4+3}{n^3+4n}}(3-2)^{n} = \sqrt{\frac{n^4+3}{n^3+4n}}[/m]
Этот ряд расходится, мы это уже доказали.