Задача 70500 ...
Условие
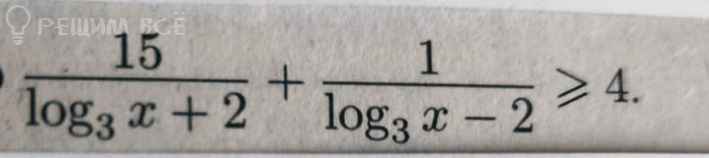
Решение
{ log_3 (x) ≠ -2 ⇒ x ≠ 1/9
{ log_3 (x) ≠ 2 ⇒ x ≠ 9
Делаем замену: log_3 (x) = y
15/(y + 2) + 1/(y - 2) ≥ 4
15/(y + 2) + 1/(y - 2) - 4 ≥ 0
[m]\frac{15(y-2)}{(y+2)(y-2)} + \frac{y+2}{(y+2)(y-2)} - \frac{4(y+2)(y-2)}{(y+2)(y-2)} ≥ 0[/m]
[m]\frac{15y-30+y+2-4(y^2-4)}{(y+2)(y-2)} ≥ 0[/m]
[m]\frac{16y-28-4y^2+16}{(y+2)(y-2)} ≥ 0[/m]
[m]\frac{-4y^2+16y-12}{(y+2)(y-2)} ≥ 0[/m]
[m]\frac{-4(y^2-4y+3)}{(y+2)(y-2)} ≥ 0[/m]
Делим всё неравенство на -4, при этом знак неравенства меняется.
[m]\frac{y^2-4y+3}{(y+2)(y-2)} ≤ 0[/m]
Раскладываем числитель на множители:
y^2 - 4y + 3 = 0
(y - 3)(y - 1) = 0
[m]\frac{(y - 3)(y - 1)}{(y+2)(y-2)} ≤ 0[/m]
По методу интервалов у нас есть 4 особые точки:
y1 = -2; y2 = 2, и в обеих точках дробь не существует.
y3 = 1; y4 = 3
y ∈ (-2; 1] U (2; 3]
log_3 (x) ∈ (-2; 1] U (2; 3]
x ∈ (1/9; 3] U (9; 27]