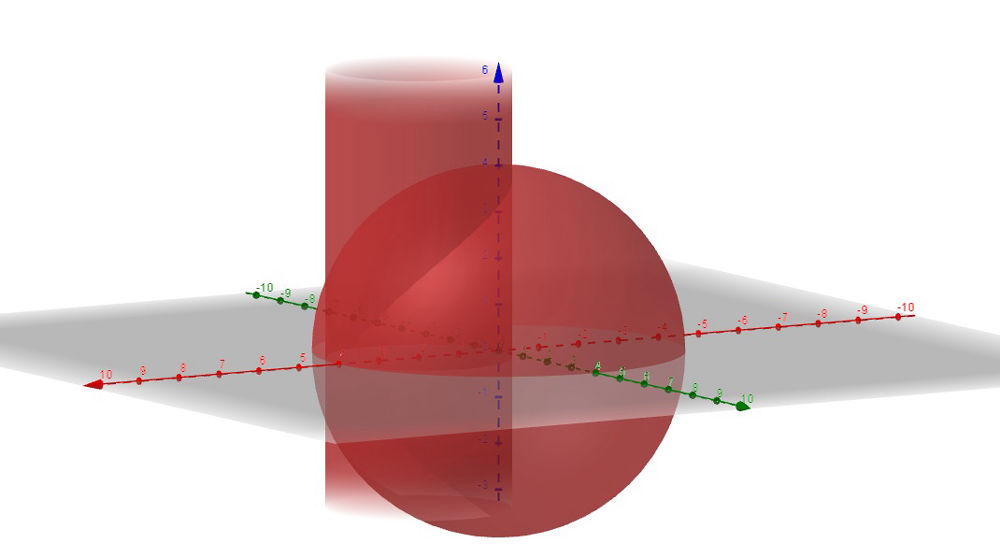
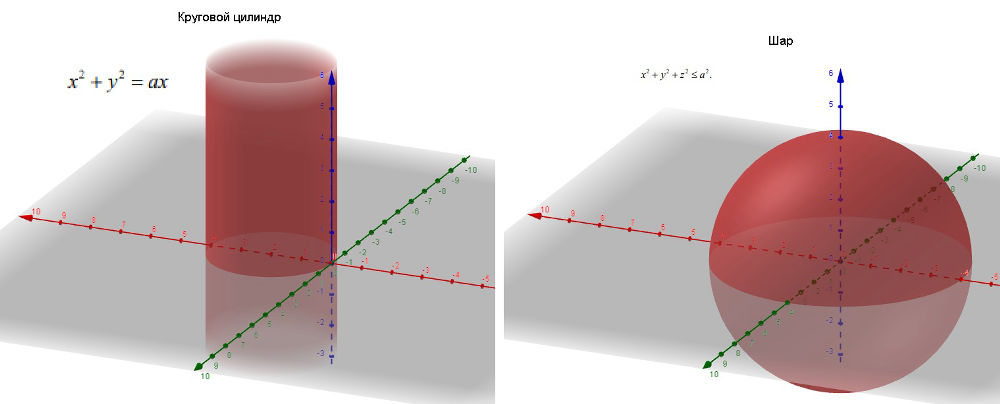
Задача 70490 ...
Условие
x^2+y^2 = ax, отсеченной x^2+y^2+z^2 ≤ a^2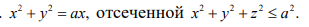
Решение
x^2+y^2=ax
(x-(a/2))^2+y^2=(a/2)^2- круговой цилиндр
Находим линию пересечения
[m]\left\{\begin {matrix}x^2+y^2=ax\\x^2+y^2+z^2=a^2\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}x^2+y^2=ax\\ax+z^2=a^2\end {matrix}\right.[/m]
[m]z^2+ax=a^2[/m] - парабола в плоскости xOz
Линия проектируется на плоскость yOz
Тогда для вычисления площади поверхности применяем формулу
[m]S= ∫ ∫ _{D_{yz}}\sqrt{1+(\frac{ ∂x }{ ∂y })^2+(\frac{ ∂x }{ ∂z })^2}dydz[/m]
(x-(a/2))^2=(a/2)^2-y^2
x-(a/2)= ± sqrt((a/2)^2-y^2)
Тело симметрично, поэтому можно вычислить часть поверхности в 3 и 4 октантах
и полученный результат удвоить
x= (a/2)+sqrt((a/2)^2-y^2)
[m]\frac{ ∂x }{ ∂y }=(\frac{a}{2}+\sqrt{(\frac{a}{2})^2-y^2})`_{y}=[/m]
[m]\frac{ ∂x }{ ∂z }=0[/m]