Задача 70382 Используя предельную форму признака...
Условие
исследовать ряд на сходимость.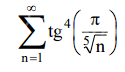
Решение
Если есть два ряда [m]\overset{\infty} {\underset{n=1}{\Sigma}} x(n)[/m] и [m]\overset{\infty} {\underset{n=1}{\Sigma}} y(n)[/m] и существует предел:
[m]\lim \limits_{n \to \infty} \frac{x(n)}{y(n)} = A ∈ (0; +oo)[/m]
То эти два ряда сходятся или расходятся одновременно.
То есть нам нужно подобрать такой ряд, чтобы он явно сходился или явно расходился, и при этом указанный предел не был ни 0, ни oo.
Сделаем замену переменной: [m]\frac{\pi}{\sqrt[5]{n}} = m[/m].
Так как n → oo, то m → 0.
Можно воспользоваться следствием из 1 Замечательного предела.
[m]\lim \limits_{x \to 0} \frac{tg(x)}{x} = 1[/m]
[m]\lim \limits_{x \to 0} \frac{tg^4(x)}{x^4} = 1[/m]
Получаем:
[m]\lim \limits_{m \to 0} \frac{tg^4(m)}{m^4} = 1[/m]
Обратная замена:
[m]m^4 = \frac{\pi^4}{\sqrt[5]{n^4}} = \frac{\pi^4}{n^{4/5}}[/m]
Это обобщенный гармонический ряд [m]\overset{\infty} {\underset{n=1}{\Sigma}} \frac{1}{n^{k}}[/m]
Он расходится при k ≤ 1 и сходится при k > 1
Так как показатель степени k = 4/5 < 1, то ряд [m]\overset{\infty} {\underset{n=1}{\Sigma}} \frac{\pi^4}{\sqrt[5]{n^4}}[/m] расходится.
Значит, и наш ряд тоже расходится.
Все решения
[m]∑( \frac{π}{\sqrt[5]{n}})^4[/m]
Этот ряд [b]расходится[/b] как обобщенный гармонический ряд вида [m]∑ \frac{1}{n^{\frac{4}{5}}}[/m]
p=4/5 < 1
[m]lim_{n → ∞ }\frac{a_{n}}{b_{n}}=lim_{n → ∞ }\frac{tg^4 \frac{π}{\sqrt[5]{n}}}{( \frac{π}{\sqrt[5]{n}})^4}=1[/m] ⇒
по признаку сравнения в предельной форме, ряды себя ведут одинаково.
Оба расходятся или оба сходятся
[m]∑( \frac{π}{\sqrt[5]{n}})^4[/m] расходится.
Значит и данный ряд расходится