Задача 70337 ...

63a8545246ce692afe75a7c4

23.03.2023 21:20:28

Дано комплексное число z. Требуется:
1) записать число z в алгебраической и тригонометрической формах;
2) найти все корни уравнения ω^3 + z = 0

5f3ea7e3faf909182968ddd9

24.03.2023 10:15:34

★

1) записать число z в алгебраической и тригонометрической формах;


[m]z=\frac{2\sqrt{2}}{1+i}=\frac{2\sqrt{2}(1-i)}{(1+i)(1-i)}=\frac{2\sqrt{2}(1-i)}{1^2-i^2}=\frac{2\sqrt{2}(1-i)}{1^2-(-1)}=\frac{2\sqrt{2}(1-i)}{2}=\sqrt{2}(1-i)=\sqrt{2}-i\cdot \sqrt{2}[/m]- алгебраическая форма

Представим число в тригонометрической форме

z=x+i*y
|z|=sqrt(x^2+y^2)
cos φ =x/|z|
sin φ =y/z

[m]z=\sqrt{2}-i\cdot \sqrt{2}[/m]
[m]x=\sqrt{2}[/m];[m]y=-\sqrt{2}[/m]

[m]|z|=\sqrt{(\sqrt{2})^2+(-\sqrt{2})^2}=\sqrt{2+2}=\sqrt{4}=2[/m]

[red][m]r=|z|=2[/m][/red]

[m]cos φ =\frac{x}{|z|}=\frac{\sqrt{2}}{2};[/m]

[m]sin φ =\frac{y}{|z|}=-\frac{\sqrt{2}}{2}[/m]

⇒ угол в 4 четверти ( косинус положительный, синус отрицательный)

φ =-π/4

Значит

[m]z=\sqrt{2}-i\cdot \sqrt{2}=2\cdot (cos(-\frac{π}{4})+i\cdot sin(-\frac{π}{4}))[/m] тригонометрическая форма
[m]z=2\cdot e^{-i\cdot \frac{π}{4}}[/m]- показательная

Можно упростить тригонометрическую форму, используя свойства четности и нечетности входящих функций косинуса и синуса

[m]z=2(cos\frac{π}{4}-i\cdot sin\frac{π}{4})[/m]


2) найти все корни уравнения

[m]ω^3 + z = 0[/m]

[m]ω^3 =-z[/m]


[m]ω=\sqrt[3]{-z}[/m]

[m]z=\sqrt{2}-i\cdot \sqrt{2}[/m] ⇒ [m]-z=-\sqrt{2}+i\cdot \sqrt{2}[/m]

[red][m]r=|-z|=2[/m][/red]

[m]cos φ =\frac{x}{|-z|}=\frac{-\sqrt{2}}{2};[/m]

[m]sin φ =\frac{y}{|z|}=\frac{\sqrt{2}}{2}[/m]

⇒ угол во 2 четверти ( синус положительный, косинус синус отрицательный)

φ =3π/4

Значит

[m]-z=-\sqrt{2}+i\cdot \sqrt{2}=2\cdot (cos(\frac{3π}{4})+i\cdot sin(\frac{3π}{4}))[/m] тригонометрическая форма

[m]-z=2(cos\frac{3π}{4}+i\cdot sin\frac{3π}{4})[/m]



По формуле Муавра:


[m] ω=\sqrt[3]{(-z)}=\sqrt[3]{2}\cdot (cos\frac{\frac{3π}{4}+2πk)}{3}+i\cdot sin\frac{\frac{3π}{4}+2πk)}{3})[/m]


k=0,1,2

при k=0

[m] ω _{1}=\sqrt[3]{2}\cdot (cos\frac{\frac{3π}{4}}{3}+i\cdot sin\frac{\frac{3π}{4}}{3}[/m]

[m] ω _{1}=\sqrt[3]{2}\cdot (cos\frac{π}{4}+i\cdot sin\frac{π}{4}[/m]



при k=1

[m] ω_{2}=\sqrt[3]{2}\cdot (cos\frac{\frac{3π}{4}+2π}{3}+i\cdot sin\frac{\frac{3π}{4}+2π}{3})[/m]

[m] ω_{2}=\sqrt[3]{2}\cdot (cos\frac{11π}{12}+i\cdot sin\frac{11π}{12}[/m]


при k=2

[m] ω_{3}=\sqrt[3]{2}\cdot (cos\frac{\frac{3π}{4}+4π}{3}+i\cdot sin\frac{\frac{3π}{4}+4π}{3})[/m]

[m] ω_{3}=\sqrt[3]{2}\cdot (cos\frac{19π}{12}+i\cdot sin\frac{19π}{12})[/m]


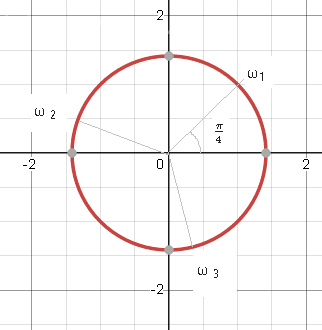
Числа [m] ω_{1}; ω_{2}; ω_{3}[/m] - корни уравнения.

Их расположение на окружности радиуса [m]\sqrt[3]{2}[/m]


Откладываем луч [m]\frac{π}{4}[/m]


Пересечение окружности и луча - точка ω_(1)


Откладываем луч [m]\frac{11π}{12}[/m]

Пересечение окружности и луча - точка ω _(2)


Откладываем луч [m]\frac{19π}{12}[/m]

Пересечение окружности и луча - точка ω _(3)


Эти три точки делят окружность на 3 равные части ( на 3 - потому что корень третьей степени)