Задача 70127 ...
Условие
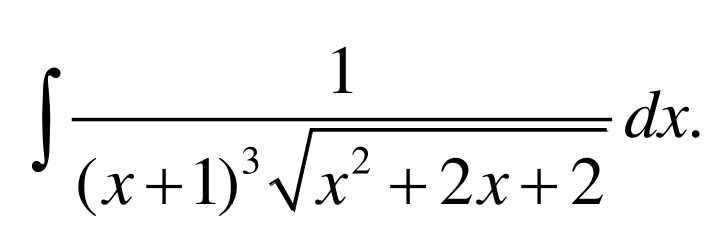
Решение
Замена
x+1=z
x=z-1
dx=dz
получим
[m] ∫\frac{1}{z^3\cdot\sqrt{z^2+1}}dz= [/m]
подстановка:
1+z^2=t^2 ⇒
z^2=t^2-1
z=sqrt(t^2-1)
dz=t/sqrt(t^2-1)
[m]= ∫(\sqrt{t^2-1})^{-3}\cdot (t^2)^{-\frac{1}{2}}\cdot \frac{t}{\sqrt{t^2-1}}dt= ∫ (t^2-1)^{-2}dt = ∫\frac{1}{(t^2-1)^2}dt= [/m]
Раскладываем дробь на простейшие
[m](t^2-1)^2=((t-1)(t+1))^2=(t-1)^2(t+1)^2[/m]
[m]\frac{1}{(t^2-1)^2}=\frac{A}{t-1}+\frac{B}{(t-1)^2}+\frac{M}{t+1}+\frac{N}{(t+1)^2} [/m]
[m]1=A(t-1)(t+1)^2+B(t+1)^2+M(t+1)(t-1)^2+N(t-1)^2[/m]
при t=1
1=4B
[b]B=1/4[/b]
при t=-1
1=4N
[b]N=1/4[/b]
при t=0
1=-A+B+M+N
при t=2
1=9A+9B+3M+N
A=-1/4
M=1/4
[m]∫\frac{1}{(t^2-1)^2}dt= \frac{1}{4}(∫\frac{(-1)}{t-1}+\frac{1}{(t-1)^2}+\frac{1}{t+1}+\frac{1}{(t+1)^2} )dt=-\frac{1}{4}ln|t-1|-\frac{1}{4(t-1)}+\frac{1}{4}ln|t+1|-\frac{1}{4(t+1)}+C [/m]
Обратный переход к переменной z и затем к переменной х
[m]=-\frac{1}{4}ln|\sqrt{z^2+1}-1|-\frac{1}{4(\sqrt{z^2+1}-1)}+\frac{1}{4}ln|\sqrt{z^2+1}+1|-\frac{1}{4(\sqrt{z^2+1}+1)}+C= [/m]
[m]=-\frac{1}{4}ln|\sqrt{x^2+2x+2}-1|-\frac{1}{4(\sqrt{x^2+2x+2}-1)}+\frac{1}{4}ln|\sqrt{x^2+2x+2}+1|-\frac{1}{4(\sqrt{x^2+2x+2}+1)}+C[/m]