Задача 69672 ...
Условие
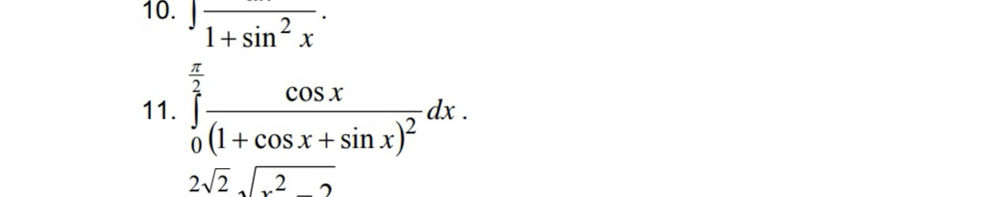
Решение
(1 + cos x + sin x)^2 = 1 + cos^2 x + sin^2 x + 2cos x + 2sin x + 2sin x*cos x = 2 + 2cos x + 2sin x + 2sin x*cos x =
= 2(1 + sin x + cos x + sin x*cos x) = 2(1 + sin x)(1 + cos x)
Можно применить универсальную тригонометрическую подстановку: tg(x/2) = t, тогда:
[m]cos(x) = \frac{1-t^2}{1+t^2}; sin(x) = \frac{2t}{1+t^2}; dx = \frac{2dt}{1+t^2}[/m]
[m]1+sin(x) = 1+\frac{2t}{1+t^2} = \frac{1+t^2+2t}{1+t^2}=\frac{(1+t)^2}{1+t^2}[/m]
[m]1+cos(x) = 1+\frac{1-t^2}{1+t^2} = \frac{1+t^2+1-t^2}{1+t^2}=\frac{2}{1+t^2}[/m]
Пределы интегрирования:
tg(0/2) = 0; tg(π/4) = 1, получаем:
[m]\int_0^1 \frac{1-t^2}{1+t^2} : (2 \cdot \frac{(1+t)^2}{1+t^2} \cdot \frac{2}{1+t^2}) \cdot \frac{2dt}{1+t^2}) =[/m]
[m]=\int_0^1 \frac{(1-t^2)(1+t^2)^2 \cdot 2}{2 \cdot (1+t)^2 \cdot 2 \cdot (1+t^2)^2}dt =[/m]
[m]= \int_0^1 \frac{1-t^2}{2 \cdot (1+t)^2}dt =\frac{1}{2} \int_0^1 \frac{1-t^2}{(1+t)^2}dt = [/m]
[m]= \frac{1}{2} (\int_0^1 \frac{1}{(1+t)^2}dt - \int_0^1 \frac{t^2}{(1+t)^2}dt) = \frac{1}{2} [-\frac{1}{1+t}|_0^1 - (\frac{t^2+t-1}{t+1} - 2ln|t+1|)|_0^1] =[/m]
[m]= \frac{1}{2} (-\frac{1}{1+1}+\frac{1}{1+0} - \frac{1+1-1}{1+1} + 2ln|1+1| + \frac{0+0-1}{0+1} - 2ln|0+1|) =[/m]
[m]= \frac{1}{2} (-\frac{1}{2}+1 - \frac{1}{2} + 2ln(2) - 1 - 2ln(1)) = \frac{1}{2} (2ln(2)-1) = ln(2) - \frac{1}{2}[/m]