Задача 69575 ...
Условие
∫ dx/(1+sqrt(3x-2))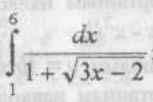
Решение
Замена переменной:
[m]\sqrt{3x+2}=t[/m] ⇒ [m]3x+2=t^2[/m]
[m]x=\frac{1}{3}(t^2-2)[/m]
[m]dx=\frac{1}{3}\cdot 2tdt[/m]
[m]dx=\frac{2}{3}tdt[/m]
[m]∫ \frac{1}{1+\sqrt{3x+2}}dx= ∫ \frac{\frac{2}{3}tdt}{1+t}=\frac{2}{3} ∫ \frac{t+1-1}{1+t}dt=\frac{2}{3} ∫ (1-\frac{1}{1+t})dt=[/m]
[m]=\frac{2}{3}t-\frac{2}{3}ln|1+t|+C=\frac{2}{3}\sqrt{3x+2}-\frac{2}{3}ln(1+\sqrt{3x+2})+C[/m]
По формуле Ньютона - Лейбница:
[m] ∫ ^{6}_{1}\frac{1}{1+\sqrt{3x+2}}dx=(\frac{2}{3}\sqrt{3x+2}-\frac{2}{3}ln(1+\sqrt{3x+2}))|^{6}_{1}=[/m]
[m]=(\frac{2}{3}\sqrt{3\cdot 6+2}-\frac{2}{3}ln(1+\sqrt{3\cdot 6+2}))-(\frac{2}{3}\sqrt{3\cdot 1+2}-\frac{2}{3}ln(1+\sqrt{3\cdot 1+2}))=\frac{2}{3}\cdot 2\sqrt{5}-\frac{2}{3}ln(1+2\sqrt{5})-\frac{2}{3}\sqrt{5}+\frac{2}{3}ln(1+\sqrt{5})=[/m]
[m]=\frac{2}{3}\sqrt{5}-\frac{2}{3}ln\frac{1+\sqrt{5}}{1+2\sqrt{5}}[/m]
Все решения
Замена:
[m]\sqrt{3x+2} = y; dy = \frac{3dx}{2\sqrt{3x+2}} = \frac{3dx}{2y}; dx = \frac{2}{3}y\ dy[/m]
[m]y(1) = \sqrt{3+2} = \sqrt{5}; y(6) = \sqrt{3 \cdot 6+2} = \sqrt{20} = 2\sqrt{5}[/m]
Подставляем в интеграл:
[m]\frac{2}{3} \cdot \int_{\sqrt{5}}^{2\sqrt{5}} \frac{y\ dy}{1+y} = \frac{2}{3} \cdot \int_{\sqrt{5}}^{2\sqrt{5}} \frac{y+1-1}{y+1}dy =[/m]
[m]= \frac{2}{3} \cdot \int_{\sqrt{5}}^{2\sqrt{5}} (1 - \frac{1}{y+1})dy = \frac{2}{3} \cdot (y - ln(y+1))|_{\sqrt{5}}^{2\sqrt{5}} =[/m]
[m]= \frac{2}{3} \cdot (2\sqrt{5} - ln(2\sqrt{5}+1) - \sqrt{5} + ln(\sqrt{5}+1)) = [/m]
[m]= \frac{2}{3} \cdot (\sqrt{5} + ln \frac{\sqrt{5}+1}{2\sqrt{5}+1})[/m]