Задача 69344 sin(x) - cos(x) = sin(2x). ...
Условие
Решение
[m]sinx-cosx=t[/m]
Возводим в квадрат
[m]sin^2x-2sinx\cdot cosx+cos^2x=t^2[/m] ⇒ [m]1-sin2x=t^2[/m]
[m]sin2x=1-t^2[/m]
получаем квадратное уравнение:
[m]t=1-t^2[/m]
[m]t^2+t-1=0[/m]
D=1+4=5
[m] t_{1}=\frac{-1-\sqrt{5}}{2} [/m] или[m] t_{2}=\frac{-1+\sqrt{5}}{2}; [/m]
Обратный переход к переменной х:
Так как ( см. метод введения вспомогательного угла)
[m] sinx-cosx=\sqrt{2}sin(x-\frac{π}{4})[/m] ⇒ [m]-\sqrt{2}≤ sinx-cosx ≤\sqrt{2}[/m]
[m] t_{1}=\frac{-1-\sqrt{5}}{2} <-\sqrt{2}[/m] ( это надо доказать: умножаем на (-2) и меняем знак [m] 2\sqrt{2} < 1+\sqrt{5}[/m] возводим в квадрат :[m]8<6+2\sqrt{5} ⇒ 2<2\sqrt{5}[/m]- очевидно)
[m] sinx-cosx=\frac{-1-\sqrt{5}}{2}[/m] не имеет корней
Получаем, что осталось решить уравнение
[m] sinx-cosx=\frac{-1+\sqrt{5}}{2}[/m] ⇒
[m]\sqrt{2}sin(x-\frac{π }{4})=\frac{(-1+\sqrt{5})}{2}[/m]
[m]sin(x-\frac{π}{4})=\frac{(-1+\sqrt{5})}{2\sqrt{2}}[/m]
не должно вызвать затруднений, непривычно, да.
Но это простейшее тригонометрическое уравнение
Решаем по формуле: [m] sin u=a[/m] и [m] 0 <a < 1[/m]
[m](x-\frac{π }{4})=(-1)^{k} arcsin\frac{-1+\sqrt{5}}{2\sqrt{2}}+πk, k ∈ [/m][b]Z[/b]
[m]x=\frac{π }{4}+(-1)^{k} arcsin\frac{-1+\sqrt{5}}{2\sqrt{2}}+πk, k ∈ [/m][b]Z[/b]- это ответ
======================
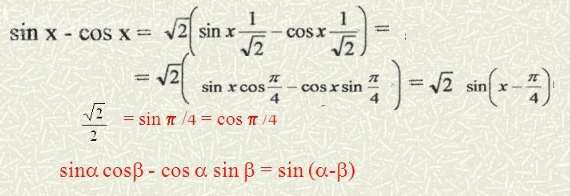
Все решения
sin x - cos x = 2sin x*cos x
Перейдем к тангенсу половинного аргумента.
[m]sin(x) = \frac{2tg(x/2)}{1+tg^2(x/2)}; cos x = \frac{1-tg^2(x/2)}{1+tg^2(x/2)}[/m]
Подставляем:
[m]\frac{2tg(x/2)}{1+tg^2(x/2)} - \frac{1-tg^2(x/2)}{1+tg^2(x/2)} = 2 \cdot \frac{2tg(x/2)}{1+tg^2(x/2)} \cdot \frac{1-tg^2(x/2)}{1+tg^2(x/2)}[/m]
[m]\frac{2tg(x/2) - 1 + tg^2(x/2)}{1+tg^2(x/2)}= \frac{4tg(x/2) \cdot (1-tg^2(x/2))}{(1+tg^2(x/2))^2}[/m]
Замена tg(x/2) = y
[m]\frac{y^2 + 2y - 1}{1+y^2}= \frac{4y (1-y^2)}{(1+y^2)^2}[/m]
Умножаем на (1 + y^2)^2
(y^2 + 2y - 1)(1+y^2) = 4y (1 - y^2)
y^4 + 2y^3 - y^2 + y^2 + 2y - 1 = -4y^3 + 4y
y^4 + 6y^3 - 2y - 1 = 0
Как это решать, я честно - не знаю. Вольфрам Альфа помог.
Это уравнение имеет 2 иррациональных корня:
[m]y1 = tg(x/2) = \frac{1}{2}(-3- \sqrt{5} - \sqrt{22+10\sqrt{5}}) ≈ -5,9482[/m]
x1 = -2arctg(5,9482) + π*n, n ∈ Z ≈ -2,8085 + πn, n ∈ Z
[m]y2 = tg(x/2) = \frac{1}{2}(-3- \sqrt{5} + \sqrt{22+10\sqrt{5}}) ≈ 0,7121[/m]
x2 = 2arctg(0,7121) + πk, k ∈ Z ≈ 1,2376 + πk, k ∈ Z
Самое главное - arctg(y) никак не выражаются через π.
Поэтому тригонометрическими преобразованиями это уравнение решить невозможно.
Скорее всего, в задании ошибка.
Или это олимпиадная задача, и предполагается, что вы умеете решать уравнения 4 степени.


