Задача 69217 Исследовать функцию и построить ее...
Условие
Y=1-x/3x
Решение
1) Область определения: x ≠ 0
D(X) = (-oo; 0) U (0; +oo)
2) Вертикальная асимптота: x = 0
3) Пересечение с осями координат.
Пересечения с осью Oy нет, так как x ≠ 0.
Пересечение с осью Ox:
y(x) = 0
[m]\frac{1 - x}{3x} = 0[/m]
x = 1
4) Знаки функции:
При x < 0 будет y < 0;
При x ∈ (0; 1) будет y > 0;
При x > 1 будет y < 0
5) Четность: Не четная и не нечетная.
6) Периодичность: Не периодическая.
7) Критические точки 1 порядка. y'(x) = 0
Экстремумы, промежутки монотонности.
[m]y'(x) = \frac{(-1) \cdot 3x - (1 - x) \cdot 3}{9x^2} = \frac{-3x - 3 + 3x}{9x^2} = \frac{-3}{9x^2} = \frac{-1}{3x^2} = 0[/m]
Это уравнение решений не имеет, значит, функция монотонна.
При любом x ∈ (-oo; 0) U (0; +oo) будет y'(x) < 0
Значит, функция всюду убывает.
8) Критические точки 2 порядка. y'' = 0
Точки перегиба, промежутки выпуклости и вогнутости.
[m]y''(x) = \frac{0- (-1) \cdot 6x}{9x^4} = \frac{2}{3x^3} = 0[/m]
Это уравнение решений не имеет, значит, точек перегиба нет.
При x < 0 будет y''(x) < 0 - функция выпуклая (вверх).
При x > 0 будет y''(x) > 0 - функция вогнутая (выпуклая вниз).
9) Наклонные асимптоты.
f(x) = kx + b
[m]k = \lim \limits_{x \to \infty} \frac{y(x)}{x} = \lim \limits_{x \to \infty} \frac{1 - x}{3x^2} = 0[/m]
Значит, наклонная асимптота - горизонтальная.
[m]b = \lim \limits_{x \to \infty} y(x)-kx = \lim \limits_{x \to \infty} \frac{1 - x}{3x} - 0 = -\frac{1}{3}[/m]
f(x) = -1/3
10) Область значений:
E(Y) = (-oo; -1/3) U (-1/3; +oo)
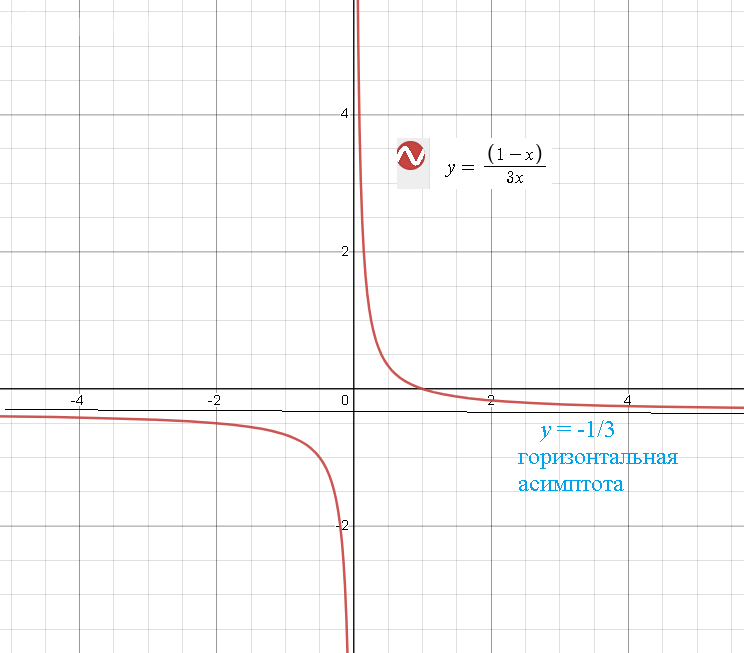
11) График.
Горизонтальная асимптота показана синим.
Все решения
Прямая x=0 ( ось Оу) - вертикальная асимптота, так как lim_(x → 2)f(x)=lim_(x → 2)(1-х)/(3x)= ∞
Прямая y=-1/3 - горизонтальная асимптота, так как lim_(x → ∞ )f(x)=lim_(x → ∞ )(1-х)/(3x)=-1/3
Выносим х за скобки в числителе х и сокращаем на него
lim_(x → ∞ )(1-х)/(3x)=lim_(x → ∞ )x*((1/x)-1)/3*x=lim_(x → ∞ )((1/x)-1)/3= -1/3
Функция не является ни чётной, ни нечётной, так как область определения не симметрична относительно 0
Находим производную:
y`=((1-x)`·(3x)–(1-x)·(3x)`)/(3x)^2
y`=((-1)·(3х)–(1-х)·3)/(3x)^2
y`=(-3)/(3x)^2
[b]y` < 0[/b] на (– ∞;0) и на (0;+ ∞ )
Функция убывает на (– ∞;0) и на (0;+ ∞ )
Нет точек экстремума.
y``=((-1/3x^2))`
y``=(-1*3x^(-2))`
y``=-1*3*(-2)*x^(-3)
y``=6/x^3
y``<0 на (– ∞;0)
y`` > 0 на (0;+ ∞ )
На (– ∞;0) функция выпукла вверх ( ∩ ) как парабола y=-x^2, у которой y``=-2 <0
На (0;+ ∞ ) функция выпукла вниз ( ∪ ) как парабола y=x^2, у которой y``=2 >0
График см. рис.