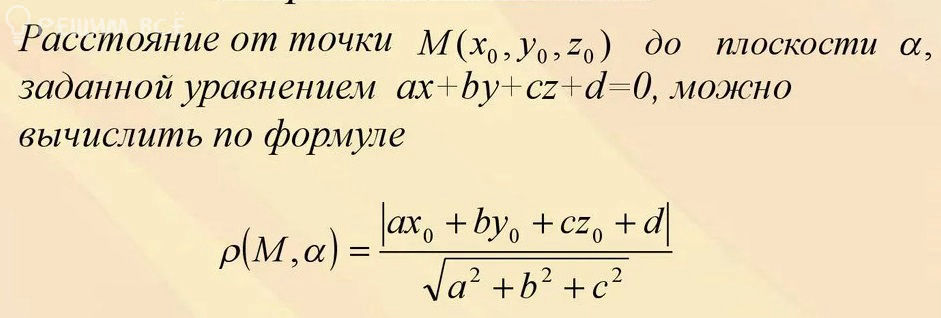Задача 68818 11-20. Даны координаты вершин пирамиды...
Условие
1) синус угла между ребром А1, A4 и гранью А1, A2,A3.
2) площадь грани А1,A2,A3.
3) объем пирамиды А1,A2,A3,A4.
4) длину высоты, опущенной из точки А4 на грань А1А2А3;
5) координаты точки А5, симметричной точке А4 относительно грани
A1A2A3.
17 номер
17. A1 (2;4; -3), A2 (2; 5; -4), A3(-2; 2; 1), A4 (-3; 0; -1).
Решение
vector{A_(1)A_{3}}=(-2-2;2-4;1-(-3))=(-4;-2;4)
vector{A_(1)A_{4}}=(-3-2;0-4;-1-(-3))=(-5;-4;4)
Пусть M (x;y;z) - произвольная точка плоскости A_(1)A_(2)A_(3)
Тогда векторы
vector{A_(1)M}=(x-2;y-4;z-(-3))=(x-2;y-4;z+3)
vector{A_(1)A_{2}}=(0;1;-1)
vector{A_(1)A_{3}}=(-4;-2;4)
лежат в одной плоскости, значит компланарны.
Условие компланарности - равенство нулю смешанного произведения векторов.
[m](\vec{A_{1}M},\vec{A_{1}A_{2}},\vec{A_{1}A_{3}})=\begin {vmatrix} x-2&y-4&z+3\\0&1&-1\\-4&-2&4\end {vmatrix}[/m]
Раскрываем определитель, получаем
[m]=х+2у+2z-4[/m]
Приравниваем к 0 и получаем уравнение плоскости [m]A_{1}A_{2}A_{3}[/m]
[m]=х+2у+2z-4=0[/m]
Нормальный вектор плоскости [m]A_{1}A_{2}A_{3}[/m]
[m]\vec{n}=(1;2;2)[/m]
Направляющий вектор прямой [m]A_{1}A_{4}[/m]
[m]\vec{A_{1}A_{4}}=(-5;-4;4)[/m]
Находим косинус угла между векторами
[m]\vec{n}=(1;2;1)[/m] и [m]\vec{A_{1}A_{4}}=(1;1;3)[/m]
[m]\vec{n}\cdot \vec{A_{1}A_{4}}=-5\cdot 1+(-4)\cdot 1+4\cdot 3=3[/m]
[m]|\vec{n}|=\sqrt{1^2+2^2+2^2}=\sqrt{9}=3[/m]
[m]|\vec{A_{1}A_{4}}|=\sqrt{(-5)^2+(-4)^2+4^2}=sqrt{57}[/m]
[m]cos ∠( \vec{n}, \vec{A_{1}A_{4}})=\frac{6}{\sqrt{6}\cdot \sqrt{11}}=\frac{3}{3\cdot \sqrt{57}}=\frac{1}{\sqrt{57}}[/m]
Угол φ между прямой и плоскостью дополняет угол между векторами, поэтому синус дополнительного угла и есть найденный косинус
[m]sin φ =sin(90 °- ∠ \vec{n}, \vec{A_{1}A_{4}}))=cos∠( \vec{n}, \vec{A_{1}A_{4}})=\frac{1}{\sqrt{57}}[/m]
2)
[m]S_{A_{1}A_{2}A_{3}}=\frac{1}{2}|\vec{A_{1}A_{2}} × \vec{A_{1}A_{3}}|[/m]
Находим векторное произведение векторов : [m]\vec{A_{1}A_{2}}[/m] и [m]\vec{A_{1}A_{3}}[/m]
[m]\vec{A_{1}A_{2}} × \vec{A_{1}A_{3}}]\begin {vmatrix} \vec{i}&\vec{j}&\vec{k}\\0&1&-1\-4&-2&4\end {vmatrix}=2\vec{i}+4\vec{j}+4\vec{k}[/m]
[m]S_{A_{1}A_{2}A_{3}}=\frac{1}{2}\sqrt{2^2+4^2+4^2}=\sqrt{36}=6[/m]
3)
[m]V=\frac{1}{6}|(\vec{A_{1}A_{2}},\vec{A_{1}A_{3}},\vec{A_{1}A_{4}})|[/m]
[m](\vec{A_{1}A_{2}},\vec{A_{1}A_{3}},\vec{A_{1}A_{4}})=\begin {vmatrix}0&1&-1\\-4&-2&4\\-5&-4&4\end {vmatrix}=...=(-10)[/m]
[m]V=\frac{1}{6}|-10|=\frac{5}{3}[/m]
5)
4)
Найдем расстояние от точки [m]A_{4}[/m] до плоскости [m]A_{1}A_{2}A_{3}[/m] :
[m] ρ =\frac{|-3+2\cdot 0+ 2\cdot 1-4|}{\sqrt{1^2+2^2+2^2}}=\frac{|-5|}{3}=\frac{5}{3}[/m]
По формуле: