Задача 68548 log2log4x+log4log2x<=-4 метод...
Условие
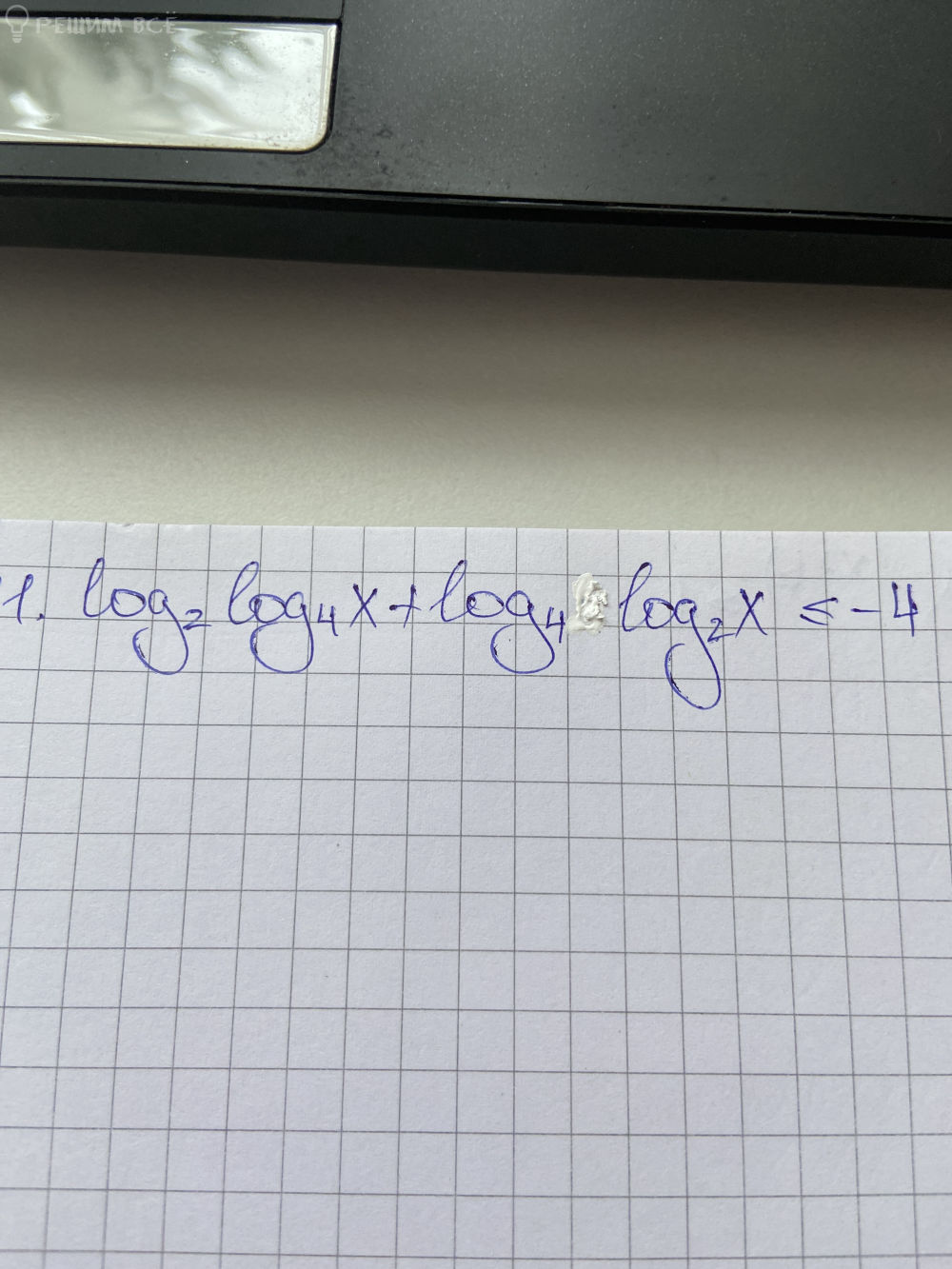
Решение
ОДЗ:
[m]\left\{\begin {matrix}x>0\\log_{4}x>0\\log_{2}x >0\end {matrix}\right.[/m] ⇒
[m]\left\{\begin {matrix}x>0\\log_{4}x>log_{4}1\\log_{2}x >log_{2}1\end {matrix}\right.[/m]
Логарифмическая функция с основанием 2 и с основанием 4 монотонно возрастающая, поэтому
[m]\left\{\begin {matrix}x>0\\x>1\\x >1\end {matrix}\right.[/m]
ОДЗ:[red] x>1[/red]
Так как
[m]log_{2}(log_{2^2}x)+ log_{2^2}(log_{2}x ) ≤ -4[/m]
и по свойствам логарифма степени:
[m]log_{2}(\frac{1}{2}log_{2}x)+ \frac{1}{2}log_{2}(log_{2}x) ≤ -4[/m]
[m]log_{2}(\frac{1}{2})+log_{2}(log_{2}x)+ \frac{1}{2}log_{2}(log_{2}x) ≤ -4[/m]
[m]-1+ \frac{3}{2}log_{2}(log_{2}x) ≤ -4[/m]
[m] \frac{3}{2}log_{2}(log_{2}x ) ≤ -3[/m]
[m] log_{2}(log_{2}x) ≤ -2[/m]
[m] log_{2}(log_{2}x) ≤ -2\cdot log_{2}2[/m]
[m] log_{2}(log_{2}x) ≤ log_{2}\frac{1}{4}[/m]
Логарифмическая функция с основанием 2 [i]монотонно возрастающая[/i], поэтому
[m] log_{2}x ≤ \frac{1}{4}[/m]
[m] log_{2}x ≤ \frac{1}{4}\cdot log_{2}2[/m]
[m] log_{2}x ≤ log_{2}2^{\frac{1}{4}}[/m]
Логарифмическая функция с основанием 2 [i]монотонно возрастающая[/i], поэтому
[m]x ≤2^{\frac{1}{4}}[/m]
С учетом ОДЗ
о т в е т. [m](1; \sqrt[4]{2}][/m]
Здесь нет таких выражений, к которым можно применить метод рационализации
( см. таблицу)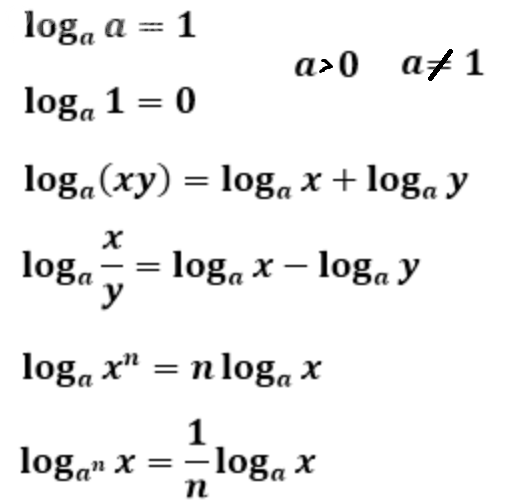

Все решения
Область определения:
{ x > 0
{ log_4(x) > 0
{ log_2(x) > 0
x > 1
Теперь решаем неравенство.
У логарифмов есть интересное свойство:
[m]log_b(a)=\frac{log_c(a)}{log_c(b)}[/m]
Причем новое основание с может быть каким угодно, главное соблюдать два ограничения: c > 0, c ≠ 1
Можно взять, например, десятичный логарифм:
[m]\frac{lg(log_4(x))}{lg(2)} + \frac{lg(log_2(x))}{lg(4)} ≤ -4[/m]
Заметим, что lg(4) = lg(2^2) = 2*lg(2).
Приводим дроби к общему знаменателю 2lg(2) = lg(4):
[m]\frac{2lg(log_4(x))}{2lg(2)} + \frac{lg(log_2(x))}{2lg(2)} ≤ -4[/m]
[m]\frac{lg(log_4(x))^2 + lg(log_2(x))}{lg(4)} ≤ -4[/m]
По правилу сложения логарифмов:
log_c(a) + log_c(b) = log_c(a*b)
[m]lg((log_4(x))^2 \cdot log_2(x)) ≤ -4lg(4)[/m]
lg(4) ≈ 0,602 > 0, поэтому при умножении знак неравенства сохранился.
[m]lg((log_4(x))^2 \cdot log_2(x)) ≤ lg(4^{-4})[/m]
Избавляемся от десятичных логарифмов:
[m](log_4(x))^2 \cdot log_2(x) ≤ 4^{-4}[/m]
Повторяем переход к десятичным логарифмам:
[m](\frac{lg(x)}{lg(4)})^2 \cdot \frac{lg(x)}{lg(2)} ≤ 2^{-8}[/m]
[m]\frac{(lg(x))^2 \cdot lg(x)}{(2lg(2))^2 \cdot lg(2)} ≤ 2^{-8}[/m]
[m]\frac{(lg(x))^3}{4(lg(2))^3} ≤ 2^{-8}[/m]
[m]\frac{(lg(x))^3}{(lg(2))^3} ≤ 2^{-6}[/m]
[m](\frac{lg(x)}{lg(2)})^3 ≤ 2^{-6}[/m]
[m]log_2(x)≤ 2^{-2}[/m]
[m]log_2(x) ≤ 1/4[/m]
[m]x ≤ 2^{1/4}[/m]
[m]x ≤ \sqrt[4]{2}[/m]
Ответ: x ∈ (1; [m]\sqrt[4]{2}[/m] ]