Задача 68544 Найдите область сходимости степенных...
Условие

Решение
1) [m]\lim \limits_{n \to \infty} \frac{a_{n+1}}{a_n} = \lim \limits_{n \to \infty} (\frac{x^{n+1}}{(n+2)2^{n+1}} : \frac{x^n}{(n+1)2^n}) = \lim \limits_{n \to \infty} (\frac{x^{n+1}}{(n+2)2^{n+1}} \cdot \frac{(n+1)2^n}{x^n}) =[/m]
[m]= \lim \limits_{n \to \infty} (\frac{x^{n+1}}{x^n} \cdot \frac{(n+1)2^n}{(n+2)2^{n+1}}) = x \cdot \lim \limits_{n \to \infty} \frac{(n+1)}{2(n+2)} = \frac{x}{2}[/m]
По признаку Даламбера, чтобы ряд сходился, должно быть:
|x/2| < 1
|x| < 2
Область сходимости ряда: (-2; 2)
Остальные делаются точно также.
2) [m]\lim \limits_{n \to \infty} \frac{a_{n+1}}{a_n} = \lim \limits_{n \to \infty} (\frac{(x-1)^{n+1}}{n+1} : \frac{(x-1)^n}{n}) =[/m]
[m]= \lim \limits_{n \to \infty} (\frac{(x-1)^{n+1}}{(x-1)^n} \cdot \frac{n}{n+1}) = (x-1) \cdot \lim \limits_{n \to \infty} \frac{n}{n+1} = x-1[/m]
|x - 1| < 1
-1 < x - 1 < 1
Область сходимости ряда: (0; 2)
3) [m]\lim \limits_{n \to \infty} \frac{a_{n+1}}{a_n} = \lim \limits_{n \to \infty} (\frac{(x-1)^{n+1}}{(n+1)!} : \frac{(x-1)^n}{n!}) = [/m]
[m]=\lim \limits_{n \to \infty} (\frac{(x-1)^{n+1}}{(x-1)^n} \cdot \frac{n!}{(n+1)!}) = (x-1) \cdot \lim \limits_{n \to \infty} \frac{1}{n+1} = 0[/m]
Предел равен 0 < 1 при любом x.
Область сходимости ряда: (-oo; +oo)
4) [m]\lim \limits_{n \to \infty} \frac{a_{n+1}}{a_n} = \lim \limits_{n \to \infty} (\frac{(x+1)^{n+1}}{3^{n+1}} : \frac{(x+1)^n}{3^n}) = [/m]
[m]=\lim \limits_{n \to \infty} (\frac{(x+1)^{n+1}}{(x+1)^n} \cdot \frac{3^n}{3^{n+1}}) = (x+1) \cdot \lim \limits_{n \to \infty} \frac{1}{3} = \frac{x+1}{3}[/m]
|(x + 1)/3| < 1
|x + 1| < 3
-3 < x + 1 < 3
Область сходимости ряда: (-4; 2)
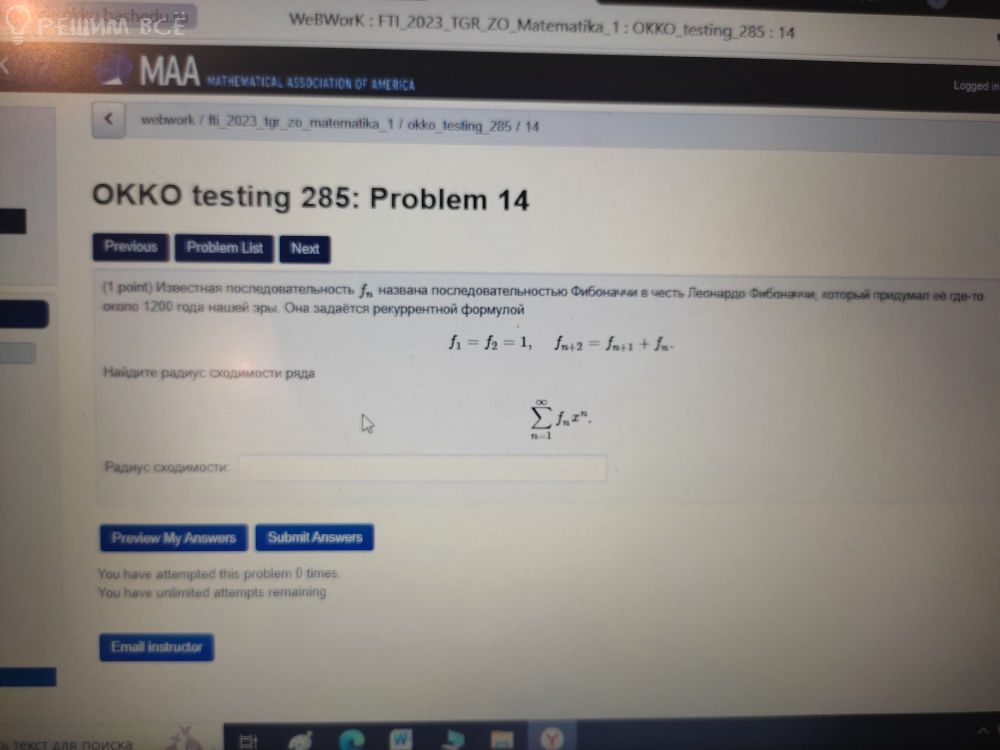
14) Нереккурентная формула ряда Фибоначчи:
[m]f(n) = \frac{((1 + \sqrt{5})/2)^n - ((1 - \sqrt{5})/2)^n}{\sqrt{5}}[/m]
Формула члена функционального ряда:
[m]a_n = f(n)x^n = x^n \cdot \frac{((1 + \sqrt{5})/2)^n - ((1 - \sqrt{5})/2)^n}{\sqrt{5}} = [/m]
[m] = \frac{x^n}{\sqrt{5}} \cdot ((\frac{1 + \sqrt{5}}{2})^n - (\frac{1 - \sqrt{5}}{2})^n) = \frac{x^n}{\sqrt{5}} \cdot \frac{(1 + \sqrt{5})^n - (1 - \sqrt{5})^n}{2^n}[/m]
По признаку Даламбера:
[m]\lim \limits_{n \to \infty} \frac{a_{n+1}}{a_n} = \lim \limits_{n \to \infty} (\frac{x^{n+1}}{\sqrt{5}} \cdot \frac{(1 + \sqrt{5})^{n+1} - (1 - \sqrt{5})^{n+1}}{2^{n+1}}) : (\frac{x^n}{\sqrt{5}} \cdot \frac{(1 + \sqrt{5})^n - (1 - \sqrt{5})^n}{2^n}) =[/m]
[m]= \lim \limits_{n \to \infty} \frac{x^{n+1}}{\sqrt{5}} \cdot \frac{(1 + \sqrt{5})^{n+1} - (1 - \sqrt{5})^{n+1}}{2^{n+1}} \cdot \frac{\sqrt{5}}{x^n} \cdot \frac{2^n}{(1 + \sqrt{5})^n - (1 - \sqrt{5})^n} =[/m]
[m]= \lim \limits_{n \to \infty} \frac{x^{n+1}}{x^n} \cdot \frac{2^n}{2^{n+1}} \cdot \frac{(1 + \sqrt{5})^{n+1} - (1 - \sqrt{5})^{n+1}}{(1 + \sqrt{5})^n - (1 - \sqrt{5})^n} =[/m]
[m]= \frac{x}{2} \cdot \lim \limits_{n \to \infty} \frac{(1 + \sqrt{5})^{n+1} - (1 - \sqrt{5})^{n+1}}{(1 + \sqrt{5})^n - (1 - \sqrt{5})^n} = P[/m]
Чтобы решить этот предел, упростим знаменатель:
[m](1 + \sqrt{5})^n - (1 - \sqrt{5})^n=(1 - \sqrt{5})^n \cdot (\frac{(1 + \sqrt{5})^n}{(1 - \sqrt{5})^n} - 1) = [/m]
[m]= (1 - \sqrt{5})^n \cdot ((\frac{1 + \sqrt{5}}{1 - \sqrt{5}})^n - 1) = (1 - \sqrt{5})^n \cdot ((1 + \frac{2\sqrt{5}}{1 - \sqrt{5}})^n - 1)[/m]
Точно также упростим числитель:
[m](1 + \sqrt{5})^{n+1} - (1 - \sqrt{5})^{n+1} = (1 - \sqrt{5})^{n+1} \cdot ((1 + \frac{2\sqrt{5}}{1 - \sqrt{5}})^{n+1} - 1)[/m]
Получаем предел:
[m]P = \frac{x}{2} \cdot \lim \limits_{n \to \infty} ((1 - \sqrt{5})^{n+1} \cdot ((1 + \frac{2\sqrt{5}}{1 - \sqrt{5}})^{n+1} - 1)) : ((1 - \sqrt{5})^n \cdot ((1 + \frac{2\sqrt{5}}{1 - \sqrt{5}})^n - 1)) = [/m]
[m] = \frac{x}{2} \cdot \lim \limits_{n \to \infty} (\frac{(1 - \sqrt{5})^{n+1}}{(1 - \sqrt{5})^n} \cdot \frac{(1 + \frac{2\sqrt{5}}{1 - \sqrt{5}})^{n+1} - 1}{(1 + \frac{2\sqrt{5}}{1 - \sqrt{5}})^n - 1}) =[/m]
[m] = \frac{x}{2} \cdot \lim \limits_{n \to \infty} (\frac{(1 - \sqrt{5})^{n+1}}{(1 - \sqrt{5})^n} \cdot \frac{(1 + \frac{2\sqrt{5}}{1 - \sqrt{5}})^{n+1}}{(1 + \frac{2\sqrt{5}}{1 - \sqrt{5}})^n}) =[/m]
[m]=\frac{x}{2} \cdot (1 - \sqrt{5}) \cdot (1 + \frac{2\sqrt{5}}{1 - \sqrt{5}})= \frac{x}{2} \cdot (1 - \sqrt{5} + 2\sqrt{5}) = \frac{x}{2} \cdot (1 + \sqrt{5})[/m]
|x*(1 + sqrt(5))/2| < 1
|x| < 2/(1 + sqrt(5))
Область сходимости ряда: (-2/(1 + sqrt(5)); 2/(1 + sqrt(5)))