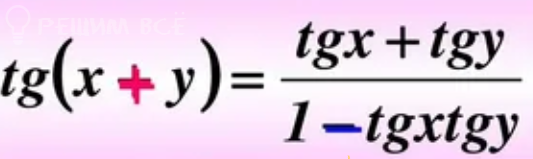Задача 67997 Найдите границу за правилом...
Условие
Расписать немного. Спасибо
Решение
[m]x-\frac{π}{4}=t[/m] ⇒ [m]x=t+\frac{π}{4}[/m]
[m]x → \frac{π}{4}[/m] ⇒ [m]t →0[/m]
[m]lim_{x →\frac{π}{4}}\frac{1-tgx}{cos2x}= lim_{t →0}\frac{1-tg(t+\frac{π}{4})}{cos2\cdot (t+\frac{π}{4})}= [/m] формула ( см. скрин)
[m] =lim_{t →0}\frac{1-\frac{tgt+tg\frac{π}{4}}{1-tgt\cdot tg\frac{π}{4}}}{cos (2t+\frac{π}{2})}= [/m]
применяем формулы приведения и табличное значение [m]tg]\frac{π}{4}=1[/m]
[m] =lim_{t →0}\frac{1-\frac{tgt+1}{1-tgt}}{sin2t}= [/m]
[m] =lim_{t →0}\frac{\frac{1-tgt-tgt-1}{1-tgt}}{(-sin2t)}=lim_{t →0}\frac{(-2tgt)}{(1-tgt)\cdot(- sin2t)}=lim_{t →0}\frac{(-2tgt)}{ (-sin2t)}=lim_{t →0}\frac{(-2t)}{(- 2t)}=1 [/m]
[m]lim_{t →0} (1-tgt)=1-tg0=1[/m]
[m]tgt ∼ t[/m] при [m] t → 0[/m]
[m]sin2t ∼ 2t[/m] при [m] t → 0[/m]
[red]2 способ[/red]
[m]lim_{x →\frac{π}{4}}\frac{1-tgx}{cos2x}= \frac{1-tg\frac{π}{4}}{cos(2\cdot \frac{π}{4})}=\frac{0}{0}=[/m]
неопределенность 0/0
[b]Применяем правило Лопиталя[/b] для вычисления предела:
[m]lim_{x →\frac{π}{4}}\frac{(1-tgx)`}{(cos2x)`}=lim_{x →\frac{π}{4}}\frac{(0-\frac{1}{cos^2x})}{(-sin2x)\cdot (2x)`}=lim_{x →\frac{π}{4}}\frac{(-\frac{1}{cos^2x})}{(-2sin2x)}=\frac{(-\frac{1}{cos^2\frac{π}{4}})}{(-2sin(2\cdot \frac{π}{4}))}=\frac{(-\frac{1}{\frac{1}{2}})}{(-2sin\frac{π}{2})}=1[/m]