Задача 67577 ...
Условие
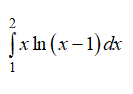
Решение
Это несобственный интеграл, придется решать через предел.
Сначала решаем неопределённый интеграл, его можно взять по частям:
[m] \int x \ln(x-1) dx = |u= \ln(x-1); dv = x dx; du = \frac{1}{x-1} dx; v = \frac{x^2}{2}| =[/m]
[m]= \frac{x^2}{2}\ln(x-1) - \int \frac{x^2}{2(x-1)} dx=\frac{x^2}{2}\ln(x-1) - \frac{1}{2}\int \frac{x^2-x+x-1+1}{x-1} dx=[/m]
[m] = \frac{x^2}{2}\ln(x-1) - \frac{1}{2}\int (x+1 + \frac{1}{x-1}) dx=\frac{x^2}{2}\ln(x-1) - \frac{1}{2}(\frac{x^2}{2} + x + \ln(x-1)) = \frac{x^2-1}{2}\ln(x-1) - \frac{x^2}{4} - \frac{x}{2}[/m]
Теперь вычисляем определенный несобственный интеграл:
[m]\int_1^2 x \ln(x-1) dx = \frac{x^2-1}{2}\ln(x-1) - \frac{x^2}{4} - \frac{x}{2} |_1^2 = \frac{2^2-1}{2}\ln(2-1) - \frac{2^2}{4} - \frac{2}{2} - (\frac{1^2-1}{2}\ln(1-1) - \frac{1^2}{4} - \frac{1}{2})[/m]
Так как ln(0) стремится к -oo, то переходим к пределу:
[m]\int_1^2 x \ln(x-1) dx = \frac{3}{2}\ln(1) - \frac{4}{4} - \frac{2}{2} - \lim \limits_{x \to 1}\frac{x^2-1}{2}\ln(x-1) + \frac{1}{4} + \frac{1}{2} =0 - 1 - 1 - \lim \limits_{x \to 1}\frac{x^2-1}{2}\ln(x-1) + \frac{1}{4} + \frac{1}{2}[/m]
Вычислим предел отдельно:
[m]\lim \limits_{x \to 1}\frac{x^2-1}{2}\ln(x-1) = \lim \limits_{x-1 \to 0}\frac{(x-1)(x+1)}{2}\ln(x-1) = \lim \limits_{x-1 \to 0}((x-1)\ln(x-1)) \cdot \lim \limits_{x \to 1}\frac{x+1}{2}[/m]
По одному из следствий из 2 Замечательного предела:
[m]\lim \limits_{z \to 0}(z \cdot \ln(z)) = 0[/m]
Поэтому весь предел равен 0. В итоге получаем:
[m]\int_1^2 x \ln(x-1) dx = 0 - 1 - 1 - 0 + \frac{1}{4} + \frac{1}{2} = -2 + \frac{3}{4} = -\frac{5}{4} = -1,2[/m]
[b]Ответ: -1,2[/b]