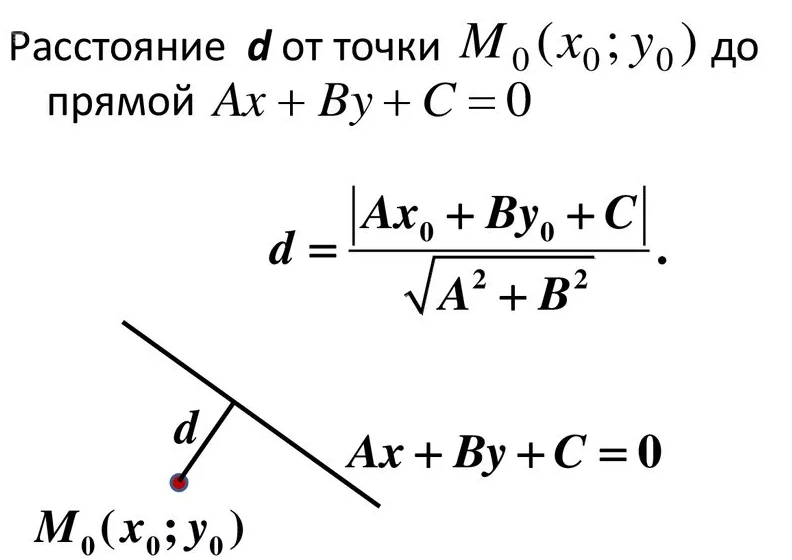Задача 67178 [b]Прямая l является биссектрисой...
Условие
[/b]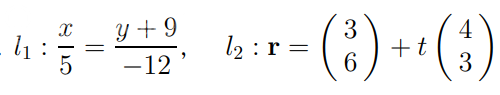
Решение
Значит, надо хорошо разбираться в том, какие виды уравнений прямой существуют.
[m]l_{1}:\frac{x}{5}=\frac{y+9}{-12}[/m]- каноническое уравнение прямой проходящей через точку с[i] направляющим[/i] вектором
vector{q}=(5;-12)
Запишем общее уравнение прямой [m]l_{1}[/m]
Для это применяем основное свойство пропорции.
Произведение крайних членов пропорции равно произведению крайних:
-12х=5*(y+9)
[b]12x+5y+45=0[/b] - общее уравнение прямой [m]l_{1}[/m]
[i]Нормальный[/i] вектор прямой vector{n_(1)}=(12;5)
Запишем уравнение этой прямой как уравнение с [i]угловым коэффициентом k[/i]
Для этого выразим y:
[b]5y=-12x-45[/b]
Делим на 5
[b]y=-2,4x-9[/b]
[i]угловой коэффициент[/i] [m]k_{1}=-2,4[/m]
[m]l_{2}:\vec{r}=[/m][m](\begin {matrix} 3\\6\end {matrix})[/m]+[m]t(\begin {matrix} 4\\3\end {matrix})[/m]-векторно-параметрическое уравнение прямой проходящей через точку (3;6)
с направляющим вектором vector{q_(2)}=(4;3)
которое можно записать так:
[m]\vec{r}=(3+4t; 6+3t)[/m]
или
[m]x=3+4t[/m]
[m]y=6+3t[/m]
⇒
[m]x-3=4t[/m] ⇒[m] t=\frac{x-3}{4}[/m]
[m]y-6=3t[/m] ⇒ [m] t=\frac{y-6}{3}[/m]
приравниваем правые части и получаем каноническое уравнение прямой:[m] \frac{x-3}{4}=\frac{y-6}{3}[/m]
⇒ [m]3(x-3)=4(y-6)[/m]
[blue][b][m]3x-4y+15=0[/m][/b][/blue] - [i]общее уравнение[/i] прямой [m]l_{2}[/m]
[i]Нормальный вектор[/i] прямой vector{n_(2)}=(3;-4)
[m]y=\frac{3}{4}x+\frac{15}{4}[/m]- уравнение прямой [m]l_{2}[/m] с [i]угловым коэффициентом [/i][m]k_{2}=\frac{3}{4}[/m]
Основной вопрос задачи
[b]12x+5y+45=0[/b] - общее уравнение прямой [m]l_{1}[/m]
[i]Нормальный[/i] вектор прямой vector{n_(1)}=(12;5)
[blue][b][m]3x-4y+15=0[/m][/b][/blue] - [i]общее уравнение[/i] прямой [m]l_{2}[/m]
[i]Нормальный вектор[/i] прямой vector{n_(2)}=(3;-4)
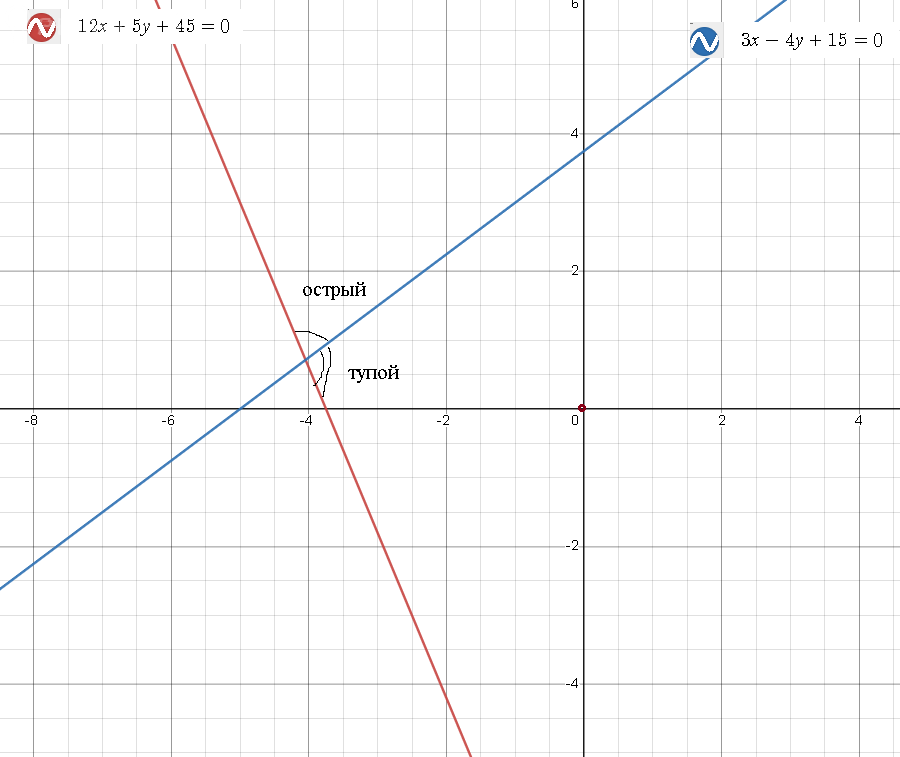
См. рис.
Пусть точка M(х;у) лежит на биссектрисе угла между прямыми.
Это значит, что расстояние [m]d_{1}[/m] этой точки до прямой [m]l_{1}[/m] равно
расстоянию [m]d_{2}[/m] этой точки до прямой [m]l_{2}[/m]
( см. формулу в приложении)
[m]d_{1}=\frac{|12x+5y+45|}{\sqrt{12^2+5^2}}[/m]
[m]d_{2}=\frac{|3x–4y+15|}{\sqrt{3^2+(-4)^2}}[/m]
[m]d_{1}=d_{2}[/m] ⇒
[m]\frac{|12x+5y+45|}{\sqrt{12^2+5^2}}=\frac{|3x–4y+15|}{\sqrt{3^2+(-4)^2}}[/m] (#)
Знак модуля раскрывается так:
[m]\frac{12x+5y+45}{\sqrt{12^2+5^2}}= ± \frac{3x–4y+15}{\sqrt{3^2+(-4)^2}}[/m]
т. е получаем два уравнения:
[m]\frac{12x+5y+45}{\sqrt{12^2+5^2}}= \frac{3x–4y+15}{\sqrt{3^2+(-4)^2}}[/m] и[m]\frac{12x+5y+45}{\sqrt{12^2+5^2}}= - \frac{3x–4y+15}{\sqrt{3^2+(-4)^2}}[/m]
[m]\frac{12x+5y+45}{13}= \frac{3x–4y+15}{5}[/m] и[m]\frac{12x+5y+45}{13}= - \frac{3x–4y+15}{5}[/m]
[m]5\cdot (12x+5y+45)=13\cdot (3x-4y+15)[/m]и [m]5\cdot (12x+5y+45)=-13\cdot (3x-4y+15)[/m]
Упрощаем
[m]60x+25y+225=39x-52y+195[/m] и [m]60x+25y+225=-39x+52y-195[/m]
[m]60x+25y+225-39x+52y-195=0[/m] и [m]60x+25y+225+39x-52y+195=0[/m]
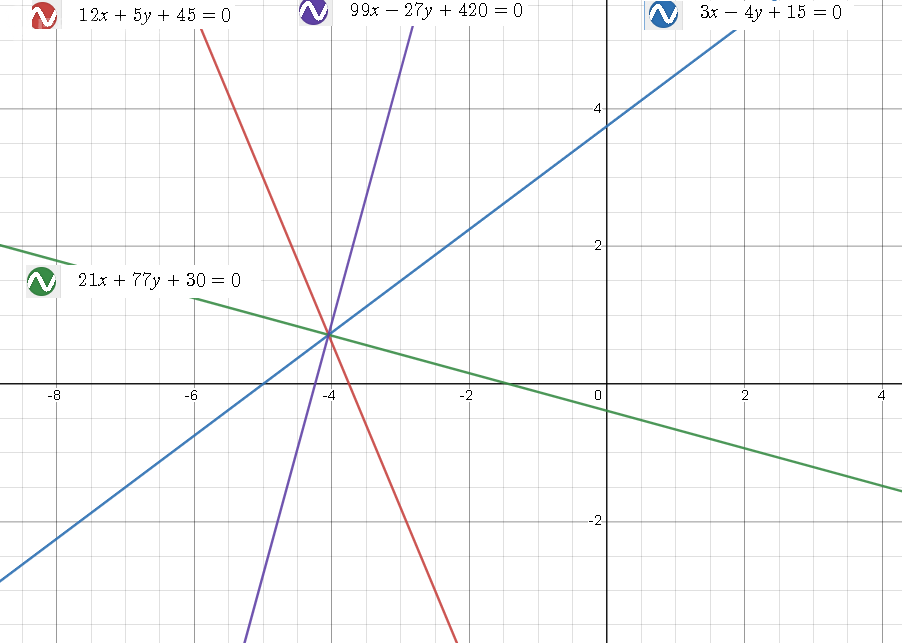
[m]21x+77y+30=0[/m] и [m]99x-27y+420=0[/m] получили две взаимно перпендикулярные прямые ( см. рис. 2)
[m]99x-27y+420=0[/m] - биссектриса острого угла. Общее уравнение с нормальным вектором (99;-27)
[m]21x+77y+30=0[/m] - биссектриса тупого угла.Общее уравнение с нормальным вектором (21;77)
Прямые перпендикулярны. Скалярное произведение нормальных векторов равно 0:
99*21+(-27)*77=0
Находим расстояние от начала координат
[m]d_{1}=\frac{|99\cdot 0-27\cdot 0+420|}{\sqrt{99^2+(-27)^2}}=\frac{420}{9\cdot \sqrt{11^2+3^2}}=\frac{140}{3\sqrt{130}}[/m]
[m]d_{2}=\frac{|21\cdot 0+77\cdot 0+30|}{\sqrt{21^2+77^2}}=\frac{30}{7\cdot{3^2+11^2}}=\frac{30}{7\sqrt{130}}[/m]
Углы между прямыми находим как углы между их нормальными векторами ( см формулу (2) справа на последнем скрине)
Если прямая [red][m]l[/m][/red]:[m]99x-27y+420=0[/m]
[i]Нормальный[/i] вектор прямой vector{n}=(99;-27)
[b]12x+5y+45=0[/b] - общее уравнение прямой [m]l_{1}[/m]
[i]Нормальный[/i] вектор прямой vector{n_(1)}=(12;5)
[blue][b][m]3x-4y+15=0[/m][/b][/blue] - [i]общее уравнение[/i] прямой [m]l_{2}[/m]
[i]Нормальный вектор[/i] прямой vector{n_(2)}=(3;-4)
[m]cos φ _{1}=\frac{99\cdot 12-27\cdot 5}{\sqrt{99^2+(-27)^2}\cdot \sqrt{12^2+5^2}}=\frac{1188-135}{9\sqrt{130}\cdot 13}=[/m]
[m]cos φ _{2}=\frac{99\cdot 3-27\cdot (-4)}{\sqrt{99^2+(-27)^2}\cdot \sqrt{3^2+(-4)^2}}=\frac{297+405}{9\sqrt{130}\cdot 5}=[/m]
Если прямая [red][m]l[/m][/red]:[m]21x+77y+30=0[/m]
[i]Нормальный[/i] вектор прямой vector{n}=(21;77)
[b]12x+5y+45=0[/b] - общее уравнение прямой [m]l_{1}[/m]
[i]Нормальный[/i] вектор прямой vector{n_(1)}=(12;5)
[blue][b][m]3x-4y+15=0[/m][/b][/blue] - [i]общее уравнение[/i] прямой [m]l_{2}[/m]
[i]Нормальный вектор[/i] прямой vector{n_(2)}=(3;-4)
[m]cos φ _{1}=\frac{21\cdot 12+77\cdot 5}{\sqrt{21^2+77^2}\cdot \sqrt{12^2+5^2}}=\frac{252+385}{7\sqrt{130}\cdot 13}[/m]
[m]cos φ _{2}=\frac{21\cdot 3+77\cdot (-4)}{\sqrt{21^2+77^2}\cdot \sqrt{3^2+(-4)^2}}=\frac{63-308}{7\sqrt{130}\cdot 5}[/m]
Можно и по формуле (1) через угловые коэффициенты находить тангенсы углов между прямыми...