Задача 65354 Нужно решить 6 уравнений из высшей...
Условие
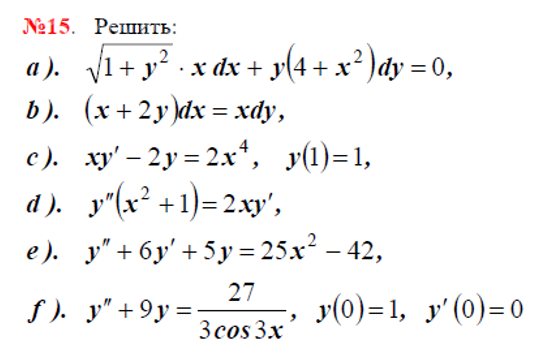
Решение
a) [m]\sqrt{1+y^2}xdx + y(4+x^2)dy = 0[/m]
[m]y(4+x^2)dy = -\sqrt{1+y^2}xdx[/m]
[m]\frac{ydy}{\sqrt{1+y^2}} = -\frac{xdx}{4+x^2}[/m]
Получили уравнение с разделёнными переменными.
Интегрируем каждую часть отдельно:
[m]\int \frac{ydy}{\sqrt{1+y^2}} = -\int \frac{xdx}{4+x^2}[/m]
[m]\int \frac{d(1+y^2)}{2\sqrt{1+y^2}} = -\int \frac{1}{2}\frac{d(4+x^2)}{4+x^2}[/m]
[m]\sqrt{1+y^2} = - \frac{1}{2}ln(4+x^2) + ln(C) = ln(\frac{C}{\sqrt{4+x^2}})[/m]
Можно остановиться на этом неявном выражении, а можно довести до вида y = F(x)
b) (x + 2y) dx = x dy
x dy = (x + 2y) dx
dy/dx = (x + 2y)/x = 2y/x + 1
y' - 2y/x = 1
Однородное уравнение 1 порядка. Решается заменой:
y/x = t; y = tx; y' = t'*x + t
t'*x + t - 2t = 1
t'*x = t + 1
dt/dx = (t+1)/x
dt/(t+1) = dx/x
ln (t+1) = ln x + ln С = ln (Cx)
t + 1 = Cx
y/x = Cx - 1
y = Cx^2 - x
c) xy' - 2y = 2x^4; y(1) = 1
y' - 2y/x = 2x^3
Неоднородное уравнение 1 порядка. Решается заменой:
y = u*v; y' = u'*v + u*v'
u'*v + u*v' - u*v/x = 2x^3
Выносим u за скобки
u'*v + u*(v' - v/x) = 2x^3
Скобку приравниваем к 0
v' - v/x = 0
dv/dx = v/x
dv/v = dx/x
ln v = ln x
v = x
Подставляем в уравнение:
u'*v + u*(v' - v/x) = 2x^3
u'*x + u*0 = 2x^3
u' = 2x^3/x = 2x^2
u = 2x^3/3 + C
y = u*x = (2x^3/3 + C)*x
Общее решение уравнения:
y = 2/3*x^4 + Cx
Подставляем известное значение y(1) = 1, находим C:
y(1) = 2/3*1^4 + C*1
1 = 2/3 + C
C = 1/3
Решение задачи Коши:
y = 2/3*x^4 + x/3
d) y''(x^2 + 1) = 2xy'
Нелинейное уравнение 2 порядка.
Решаем понижением порядка уравнения.
y' = z; y'' = z'
z'(x^2 + 1) = 2xz
dz/dx*1/z = 2x/(x^2 + 1)
dz/z = 2xdx/(x^2+1) = d(x^2 + 1)/(x^2 + 1)
ln z = ln (x^2 + 1) + ln С1 = ln (C1*x^2 + C1)
z = C1*x^2 + C1
y' = C1*x^2 + C1
y = C1*x^3/3 + C1*x + C2
e) y'' + 6y' + 5y = 25x^2 - 42
Линейное неоднородное уравнение 2 порядка
y = y_(одн) + y_(неодн)
Решаем однородное уравнение:
y'' + 6y' + 5y = 0
Характеристическое уравнение:
k^2 + 6k + 5 = 0
(k + 1)(k + 5) = 0
k1 = -1; k2 = -5
Решение однородного уравнения:
y_(одн) = C1*e^(-x) + C2*e^(-5x)
Находим частное решение неоднородного уравнения.
Правая часть: 25x^2 - 42, поэтому:
y_(неодн) = Ax^2 + Bx + C
y_(неодн)' = 2Ax + B
y_(неодн)'' = 2A
Подставляем в исходное уравнение:
2A + 6(2Ax + B) + 5(Ax^2 + Bx + C) = 25x^2 - 42
5Ax^2 + (12A + 5B)x + (2A + 6B + 5C) = 25x^2 + 0x - 42
Система по степеням x:
{ 5A = 25 (x^2)
{ 12A + 5B = 0 (x)
{ 2A + 6B + 5C = -42 (числа)
Решаем:
{ A = 5
{ 12*5 + 5B = 0 ⇒ B = -12
{ 2*5 + 6(-12) + 5C = -42 ⇒ C = 4
y_(неодн) = 5x^2 - 12x + 4
Общее решение неоднородного уравнения:
y = y_(одн) + y_(неодн)
y = C1*e^(-x) + C2*e^(-5x) + 5x^2 - 12x + 4
f) [m]y'' + 9y = \frac{27}{3cos(3x)}[/m]; y(0) = 1; y'(0) = 0
Линейное неоднородное уравнение 2 порядка
y = y_(одн) + y_(неодн)
Решаем однородное уравнение:
y'' + 9y = 0
Характеристическое уравнение:
k^2 + 9 = 0
k1 = -sqrt(3)*i; k2 = sqrt(3)*i
Решение однородного уравнения:
y_(одн) = C1*cos(3x) + C2*sin(3x)
Частное решение неоднородного уравнения я не знаю, как искать.
Вольфрам Альфа показывает такую функцию:
y_(неодн) = ln(cos(3x))*cos(3x) + 3x*sin(3x)
y = y_(одн) + y_(неодн)
y = C1*cos(3x) + C2*sin(3x) + ln(cos(3x))*cos(3x) + 3x*sin(3x)
[m]y' = -3C1*sin(3x) + 3C2*cos(3x) + \frac{-3sin(3x)*cos(3x)}{cos(3x)} - 3ln(cos(3x))*sin(3x)+ 3sin(3x) + 9x*cos(3x)[/m]
Подставляем известные значения y(0) = 1; y'(0) = 0, находим C1 и C2:
{ y(0) = C1*cos 0 + C2*sin 0 + ln(cos 0)*cos 0 + 3*0*sin 0
{ [m]y'(0) = -3C1*sin 0 + 3C2*cos 0 + \frac{-3sin 0*cos 0}{cos 0} - 3ln(cos 0)*sin 0+ 3sin 0 + 9*0*cos 0[/m]
Решаем:
{ 1 = C1*1 + C2*0 + ln 1*1 + 0
{ 0 = 0 + 3С2 + 0 - 0 + 0 + 0
Получаем:
{ C1 = 1
{ C2 = 0
Решение задачи Коши:
y = cos(3x) + ln(cos(3x))*cos(3x) + 3x*sin(3x)