Задача 65046 Задана функция распределения случайной...

6240703940eb0a5b1739b1ba

11.06.2022 15:30:15

Задана функция распределения случайной величины X
Требуется найти: а) дифференциальную функцию f (x);
б) математическое ожидание и дисперсию случайной величины X;
в) построить графики функций F(x) и f (x). N=16

5f3ea7e3faf909182968ddd9

11.06.2022 17:18:57

★

Так как [m]f (x)=F `(x)[/m]

[m]f(x)=\left\{\begin{matrix}
0,если x ≤ 16\\\frac{1}{16^2}\cdot 2\cdot (x-16)=\frac{1}{128}\cdot (x-16), если 16<x≤32 \\0, если x >32\end{matrix}\right.[/m]


По определению:
[m]M(X)=∫ ^{∞ }_{- ∞ }x\cdot f(x)dx[/m]

Так как функция задана на трех промежутках, то интеграл равен сумме интегралов по трем промежуткам (первый и последний равны 0, так как функция равна 0):

[m]M(X)= ∫ ^{32}_{16}x\cdot \frac{1}{128}(x-16)dx=\frac{1}{128}∫ ^{32}_{16}x\cdot (x-16)dx=\frac{1}{128}∫ ^{32}_{16} (x^2-16x)dx=\frac{1}{128}(\frac{x^3}{3})-16\cdot \frac{x^2}{2})|^{32}_{16}=...[/m]


По формуле:

[red]D(X)=M(X^2)-(M(X))^2[/red]

Считаем

[m]M(X^2)=∫ ^{∞ }_{- ∞ }x^2\cdot f(x)dx[/m]

Так как функция задана на трех промежутках, то интеграл равен сумме интегралов по трем промежуткам (первый и последний равны 0, так как функция равна 0):

[m]M(X)= ∫ ^{32}_{16}x^2\cdot \frac{1}{128}(x-16)dx= \frac{1}{128}∫ ^{32}_{16}(x^3-16x^2)dx=\frac{1}{128}(\frac{x^4}{4}-16\cdot\frac{x^3}{3})|^{32}_{16}=[/m]


Тогда
[m]D(X)=M(X^2)-(M(X))^2=[/m]



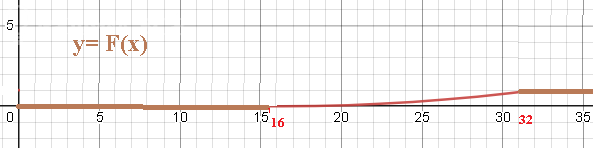
Графиком y=F(x)
на [16;32] является парабола y=(1/256)*(x-16)^2
ветви вверх,
вершина в точке (16;0)


Графиком y=f(x)
на [16;32] является прямая y=(1/128)*(x-16)

проходящая через две точки

(16;0) и (0; -16/128)



чертеж очень мелкий...

Возьмите масштаб побольше по оси Оу