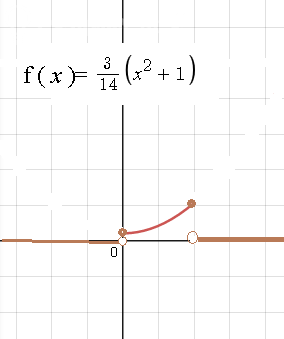Задача 65043 Непрерывная случайная величина X задана...
Условие
а) Значение постоянной C , при которой функция будет плотностью вероятности некоторой случайной величины X ;
б) Выражение функции распределения F (x);
в) Вычислить вероятность того, что случайная величина X примет значение на отрезке [a;b];
г) Найти математическое ожидание и дисперсию случайной величины X ;
д) Вычислить медиану этой случайной величины X ;
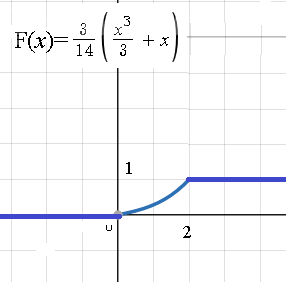
е) Построить графики функций F (x) и f (x).
Решение
[m]∫ ^{∞}_{- ∞} p(x)dx=1[/m]
и функция задана на трех промежутках, то
[m]∫ ^{+ ∞ }_{- ∞}f(x)dx=∫ ^{0 }_{- ∞}0dx+∫ ^{2}_{0} С(x^2+1)dx+∫ ^{+ ∞ }_{2} 0dx[/m]
[m]0+C\cdot (\frac{x^{3}}{3}+x)| ^{2 }_{0}+0=1[/m]
[m]C\cdot (\frac{2^{3}}{3}+2)=1[/m]
[m]C=\frac{3}{14}[/m]
По определению функция распределения :
[m]F(x)= ∫ ^{x}_{- ∞ }f(x)dx[/m]
[b]При x ≤0[/b]
[m]F(x)= ∫ ^{x}_{- ∞ }0dx=0[/m]
[b]При 0< x ≤ 2 [/b]
[m]F(x)= ∫ ^{x}_{- ∞ }f(x)dx=∫ ^{0}_{- ∞ }0dx+∫ ^{x}_{0}\frac{3}{14}(x^2+1)dx∫ ^{0}_{- ∞ }0dx+∫ ^{x}_{0}\frac{3}{14}(x^2+1)dx=\frac{3}{14}\cdot (\frac{x^{3}}{3}+x)| ^{x}_{0}=\frac{3}{14}\cdot (\frac{x^{3}}{3}+x)[/m]
[b]При x > 2 [/b]
[m]F(x)= ∫ ^{x}_{- ∞ }f(x)dx=∫ ^{0}_{- ∞ }0dx+∫ ^{2}_{0}\frac{3}{14}(x^2+1)dx+∫_{2}^ {+ ∞ }0dx=∫ ^{2}_{0}\frac{3}{14}(x^2+1)dx=\frac{3}{14}\cdot (\frac{x^{3}}{3}+x)|^{2}_{0}=1[/m]
Получаем:
[m]F(x)\left\{\begin {matrix}0, x ≤0\\\frac{3}{14}\cdot (\frac{x^{3}}{3}+x), 0<x ≤ 2\\1, x>2 \end {matrix}\right.[/m]
По формуле:
[m]P( α ≤ x ≤ β )=F( β )-F( α )[/m]
получаем:
[m]P( 0 < x <1 )=F(1 )-F(0)=\frac{3}{14}\cdot (\frac{1}{3}+1)=\frac{4}{14}=\frac{2}{7}[/m]
По определению:
[m]M(X)=∫ ^{∞ }_{- ∞ }x\cdot f(x)dx[/m]
Так как функция задана на трех промежутках, то интеграл равен сумме интегралов по трем промежуткам (первый и последний равны 0, так как функция равна 0):
[m]M(X)= ∫ ^{0}_{2}x\cdot\frac{3}{14} (x^2+1)dx=\frac{3}{14}∫ ^{0}_{2}(x^3+x)dx=...[/m] cчитайте
По формуле:
[red]D(X)=M(X^2)-(M(X))^2[/red]
Считаем
[m]M(X^2)=∫ ^{∞ }_{- ∞ }x^2\cdot f(x)dx[/m]
Так как функция задана на трех промежутках, то интеграл равен сумме интегралов по трем промежуткам (первый и последний равны 0, так как функция равна 0):
[m]M(X)= ∫ ^{0}_{2}x^2\cdot \cdot\frac{3}{14} (x^2+1)dx=\frac{3}{14}∫ ^{0}_{2}(x^4+x^2)dx=...[/m]cчитайте
Тогда
[red][m]D(X)=M(X^2)-(M(X))^2=...[/red]
Графики плотности вероятностей и функции распределения вероятностей: