Задача 64875 Найти интервалы сходимости рядов и...
Условие
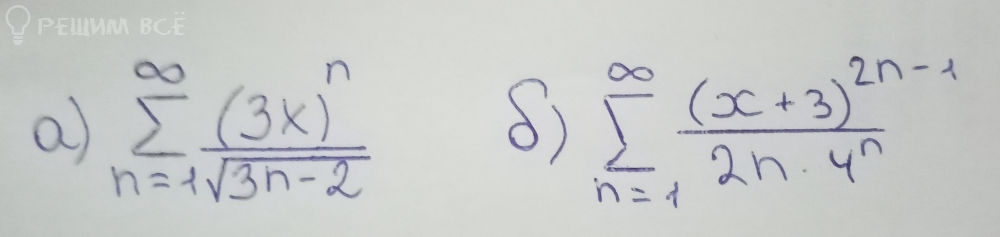
Решение
[m]a_{n}=\frac{3^{n}}{\sqrt{3n-2}}[/m]
[m] R=lim_{n → ∞ }\frac{a_{n}}{a_{n+1}}[/m]
[m]a_{n+1}=\frac{3^{n+1}}{\sqrt{3(n+1)-2}}[/m]
[m]a_{n+1}=\frac{3^{n+1}}{\sqrt{3n+1}}[/m]
[m]\frac{a_{n}}{a_{n+1}}=\frac{\frac{3^{n}}{\sqrt{3n-2}}}{\frac{3^{n+1}}{\sqrt{3n+1}}}=\frac{3^{n}}{\sqrt{3n-2}}\cdot \frac{\sqrt{3n+1}}{3^{n+1}}=\frac{\sqrt{3n+1}}{3\sqrt{3n-1}}[/m]
[m] R=lim_{n → ∞ }\frac{a_{n}}{a_{n+1}}=lim_{n → ∞ }\frac{\sqrt{3n+1}}{3\sqrt{3n-1}}=\frac{1}{3}[/m]
(-1/3;1/3) - интервал сходимости.
Проверяем сходимость на концах интервала.
x=-1/3
получаем знакочередующийся числовой ряд:
[m]∑ _{n=1}^{ ∞ }\frac{3^{n}}{\sqrt{3n-2}}\cdot (-\frac{1}{3})^{n}[/m]
Упрощаем:
[m] (-\frac{1}{3})^{n}=(-1)^{n}\cdot \frac{1}{3^{n}}[/m]
тогда
[m]∑ _{n=1}^{ ∞ }(-1)^{n}\frac{1}{\sqrt{3n-2}} - ряд сходится по признаку Лейбница:
1) [m]\frac{1}{\sqrt{3n-2}}[/m] → 0
при n → ∞
2) последовательность [m](\frac{1}{\sqrt{3n-1}})_{n=1}^{ ∞ }[/m] монотонно [i]убывающая[/i]
x=1/3
получаем знакоположительный числовой ряд:
[m]∑ _{n=1}^{ ∞ }\frac{3^{n}}{\sqrt{3n-2}}\cdot (\frac{1}{3})^{n}[/m]
Упрощаем:
[m]∑ _{n=1}^{ ∞ }\frac{1}{\sqrt{3n-2}} - ряд расходится по признаку сравнения в предельном виде
Ряд
[m]∑ _{n=1}^{ ∞ }\frac{1}{\sqrt{n}} [/m] - [i]расходится,[/i] потому что это ряд вида [m]∑ _{n=1}^{ ∞ }\frac{1}{n^{p}}[/m]
- обобщенный гармонический ряд, который сходится при p>1
и расходится при p ≤ 1
Можно применить к ряду [m]∑ _{n=1}^{ ∞ }\frac{1}{\sqrt{n}} [/m] интегральный признак
Так как
[m]lim_{n → ∞}\frac{\frac{1}{\sqrt{3n-2}}}{\frac{1}{\sqrt{n}}}=\frac{1}{\sqrt{3}} [/m]
⇒по признаку сравнения в предельном виде
ряды [m]∑ _{n=1}^{ ∞ }\frac{1}{\sqrt{3n-2}} и [m]∑ _{n=1}^{ ∞ }\frac{1}{\sqrt{n}} [/m] одновременно расходятся
б)
Так как степени х - нечетные, нельзя решать задачу таким же способом.
Находим
[m]lim_{n → ∞ }\frac{|u_{n+1}|}{|u_{n}|}=lim_{n → ∞ }\frac{\frac{|(x+3)^{2n+1}|}{2(n+)\cdot 4^{n+1}}}{\frac{|(x+3)^{2n-1}|}{2n\cdot 4^{n}}}=|x+3|^2\cdot lim_{n → ∞ }\frac{2n\cdot 4^{n}}{2(n+1)\cdot 4^{n+1}}=\frac{1}{4}|x+3|^2\cdot lim_{n → ∞}\frac{2n}{2n+2}=\frac{1}{4}\cdot |x+3|^2\cdot 1 [/m]
Если [m]\frac{1}{4}\cdot |x+3|^2 < 1 [/m]- ряд сходится абсолютно ⇒
[m]\frac{1}{2}\cdot |x+3| < 1 [/m]
⇒
[m]-2 <x+3 <2[/m] ⇒ [m]-5 < x < -1[/m]
(-5;-1) -интервал сходимости
Проверяем сходимость на концах интервала.
x=-1
получаем знакоположительный числовой ряд:
[m]∑ _{n=1}^{ ∞ }\frac{1}{2n\cdot 4^{n}}\cdot (-1+3)^{n}[/m]
Упрощаем:
[m]∑ _{n=1}^{ ∞ } \frac{2^{n}}{2n\cdot 4^{n}}[/m] - ряд сходится по признаку Даламбера:
[m]lim_{n → ∞ }\frac{a_{n+1}}{a_{n}}=lim_{n → ∞ }\frac{\frac{2^{n+1}}{2(n+1)\cdot 4^{n+1}}{\frac{2^{n}}{2n\cdot 4^{n}}=\frac{2}{4} < 1[/m]
x=-5
получаем знакочередующийся числовой ряд:
[m]∑ _{n=1}^{ ∞ }\frac{1}{2n\cdot 4^{n}}\cdot (--5+3)^{n}[/m]
Упрощаем:
[m]∑ _{n=1}^{ ∞ }(-1)^{n}\cdot \frac{2^{n}}{2n\cdot 4^{n}}[/m] -знакочередующийся ряд сходится,
сходится абсолютно , так как ряд из модулей
[m]∑ _{n=1}^{ ∞ } \frac{2^{n}}{2n\cdot 4^{n}}[/m] сходится.
Значит
[-5;-1]- область сходимости