Задача 63856 Неравенства профлиль ...
Условие
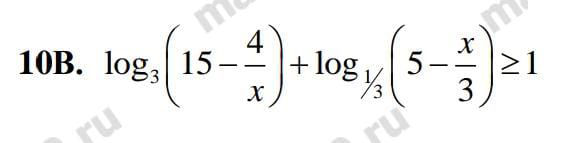
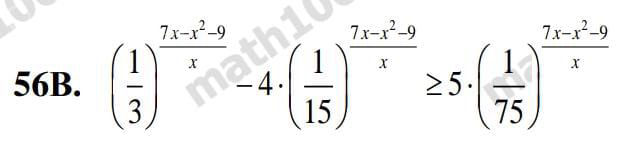
Решение
[m]\left\{\begin {matrix}15-\frac{4}{x}>0\\5-\frac{x}{3}>0\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}-\frac{4}{x}>-15\\-\frac{x}{3}>-5\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}\frac{4}{x}<15\\x < 15\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}\frac{4-15x}{x}<0\\x < 15\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}\frac{15x-4}{x}>0\\x< 15\end {matrix}\right.[/m]
[red]ОДЗ[/red]: [m]x < 0[/m] или [m] \frac{4}{15}<x < 15[/m]
По свойству логарифмов:
[m]log_{\frac{1}{3}}(5-\frac{x}{3})=log_{3^{-1}}(5-\frac{x}{3})=-log_{3}(5-\frac{x}{3})[/m]
Неравенство примет вид:
[m]log_{3}(15-\frac{4}{x})-log_{3}(5-\frac{x}{3}) ≥1 [/m]
[m]log_{3}(15-\frac{4}{x}) ≥ log_{3}(5-\frac{x}{3})+1 [/m]
[m]log_{3}(15-\frac{4}{x}) ≥ log_{3}(5-\frac{x}{3})+log_{3}3 [/m]
По свойствам логарифмов:
[m]log_{3}(15-\frac{4}{x}) ≥ log_{3}3\cdot (5-\frac{x}{3})[/m]
Логарифмическая функция с основанием 3 >1 возрастающая
[m]15-\frac{4}{x} ≥ 3\cdot (5-\frac{x}{3})[/m]
[m]15-\frac{4}{x} ≥ 15-x[/m]
[m]\frac{4}{x}-x≤0 [/m]
[m]\frac{4-x^2}{x}≤0 [/m]
[m]\frac{(x-2)(x+2)}{x}≥0 [/m]
[m]x ∈ [-2;0)\cup[2;+ ∞ )[/m]
C учетом ОДЗ:
О т в е т. [m][-2;0)\cup[2;15 )[/m]
2.
[red]ОДЗ[/red]: x ≠ 0
Замена переменной: [m] \frac{7x-x^2-9}{x}=t[/m]
Уравнение примет вид:
[m](3^{-1})^{t}-4 \cdot (15^{-1})^{t} ≥ 5\cdot ((75)^{-1})^{t}[/m]
[m](3)^{-t}-4 \cdot (15)^{-t} -5\cdot (75)^{-t} ≥ 0[/m]
[m]3^{-t}-4\cdot 3^{-t}\cdot 5^{-t}-5\cdot 3^{-t}\cdot 25^{-t}≥ 0[/m]
Раскладываем на множители:
[m]3^{-t}(1-4\cdot 5^{-t}-5\cdot (5^{-t})^2)≥ 0[/m]
[m]3^{-t}>0 [/m] при любых t
[m]1-4\cdot 5^{-t}-5\cdot (5^{-t})^2≥ 0[/m]
[m]5\cdot u^2+4\cdot u-1 ≤ 0[/m] ; [m] u=5^{-t}[/m]
D=16+20=36
[m]u_{1}=-1[/m] или [m]u_{2}=\frac{1}{5}[/m]
Решение неравенства:
[m]-1 ≤ u ≤ \frac{1}{5}[/m]
Обратная замена:
[m]-1 ≤ 5^{-t} ≤ 5^{-1}[/m]
так как [m] 5^{-t} > 0[/m]
получаем:
[m] 5^{-t} ≤ 5^{-1}[/m]
возвращаемся к переменной х:
[m] 5^{- \frac{7x-x^2-9}{x}} ≤ 5^{-1}[/m]
5>1, показательная функция [i]возрастает[/i]
[m] - \frac{7x-x^2-9}{x} ≤ -1[/m]
[m] \frac{-7x+x^2+9}{x}+1 ≤ 0[/m]
[m] \frac{-7x+x^2+9+x}{x} ≤ 0[/m]
[m] \frac{x^2-6x+9}{x} ≤ 0[/m]
[m] \frac{(x-3)^2}{x} ≤ 0[/m]
[m] x >0[/m]
О т в е т. [m] (0;+ ∞ )[/m]