Задача 63718 2. Интегрирование рациональных функций...
Условие
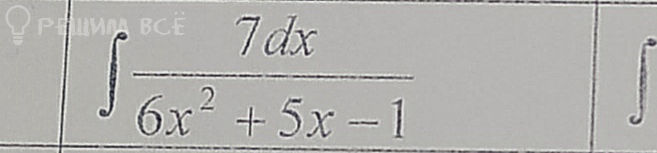
Решение
Выделяем полный квадрат
[m]6x^2+5x-1=6(x^2+\frac{5}{6}x-\frac{1}{6})=6((x+\frac{5}{12})^2-\frac{25}{144}-\frac{1}{6})=6((x+\frac{5}{12})^2-\frac{49}{144})[/m]
[m] ∫ \frac{7}{6x^2+5x-1}dx=\frac{7}{6} ∫ \frac{1}{(x+\frac{5}{12})^2-\frac{49}{144}}dx[/m]
это табличный интеграл, который считаем по формуле ( см. скрин)
[m]a^2=\frac{49}{144}[/m]
[m] ∫ \frac{7}{6x^2+5x-1}dx=\frac{7}{6} ∫ \frac{d(x+\frac{5}{12})}{(x+\frac{5}{12})^2-\frac{49}{144}}dx=\frac{7}{6} \frac{1}{2\cdot \frac{7}{12}}ln|\frac{(x+\frac{5}{12})-\frac{7}{12}}{(x+\frac{5}{12})+\frac{7}{12}}|+C=[/m]
[m]=ln|\frac{x-\frac{1}{6}}{x+1}|+C=ln|x-\frac{1}{6}|-ln|x+1|+C[/m]
можно упростить:
[m]ln|x-\frac{1}{6}|-ln|x+1|+C=ln|\frac{6x-1}{6}|-ln|x+1|+C=ln|6x-1|-ln6 -ln|x+1|+C=ln|6x-1| -ln|x+1|+C[/m]
-ln6-это константа, поэтому ее не пишем. она относится к постоянной С.
О т в е т. [m] ln|x-\frac{1}{6}|-ln|x+1|+C[/m] -
О т в е т. [m]ln|6x-1|-ln|x+1|+C[/m]
Оба ответы верные. Они совпадают с точностью до константы...
[b]2 способ[/b]
Раскладываем знаменатель на множители:
[m]6x^2+5x-1=6(x-\frac{1}{6})(x+1)=(6x-1)(x+1)[/m]
Раскладываем дробь на [b]простейшие[/b]:
[m]\frac{7}{6x^2+5x-1}=\frac{A}{6x-1}+\frac{B}{x+1}[/m]
[m]7=Ax+A+6Bx-B[/m]
[m]\left\{\begin {matrix}7=A-B\\A+6B=0\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}7+B=A\\7+B+6B=0\end {matrix}\right.[/m] ⇒
[m]\left\{\begin {matrix}A=6\\B=-1\end {matrix}\right.[/m]
[m]\frac{7}{6x^2+5x-1}=\frac{6}{6x-1}-\frac{1}{x+1}[/m]
[m] ∫ \frac{7}{6x^2+5x-1}dx= ∫ \frac{6}{6x-1}dx- ∫ \frac{1}{x+1}dx[/m]
Табличные интегралы, по формуле [m] ∫ \frac{du}{u}=ln|u|+C[/m]
[m] ∫ \frac{7}{6x^2+5x-1}dx= ∫ \frac{d(6x-1)}{6x-1}- ∫ \frac{d(x+1)}{x+1}=ln|6x-1|-ln|x+1|+C[/m]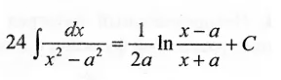
Все решения
