Задача 63441 ...
Условие
∫ 4+3x/x^2+5x+4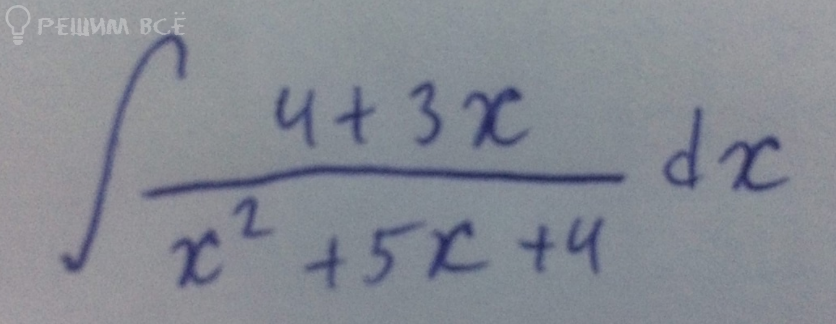
Решение
[m]x^2+5x+4=x^2+2\cdot x\cdot \frac{5}{2}+(\frac{5}{2})^2-(\frac{5}{2})^2+4=(x+\frac{5}{2})^2-\frac{9}{4}[/m]
[red]Замена переменной[/red]:
[m]x+\frac{5}{2}=t[/m]
[m]x=t-\frac{5}{2}[/m] ⇒ [m]=4+3x=4+3\cdot (t-\frac{5}{2})=4+3t-\frac{15}{2}=3t-\frac{7}{2}[/m]
[m]dx=t[/m]
Тогда
[m] ∫ \frac{4+3x}{x^2+5x+4}dx= ∫ \frac{3t-\frac{7}{2}}{(x+\frac{5}{2})^2-\frac{9}{4}}dt=[/m] [red]интеграл от суммы[/red] равен сумме интегралов:
[m]=∫ \frac{3t}{t^2-\frac{9}{4}}dt-∫ \frac{\frac{7}{2}}{t^2-\frac{9}{4}}dt=[/m]
[red]постоянный множитель[/red] можно вынести за знак интеграла:
[m]=3∫ \frac{t}{t^2-\frac{9}{4}}dt-\frac{7}{2}∫ \frac{1}{t^2-\frac{9}{4}}dt=[/m]
[red]Табличные интегралы[/red]:
[r][m] ∫ \frac{du}{u}=ln|u|+C[/m] [/r]; полагаем в первом интеграле [m]u=t^2-\frac{9}{4}[/m] тогда [m]du=2tdt[/m]; [m]tdt=\frac{1}{2}du[/m]
[r][m] ∫ \frac{dx}{x^2-a^2}=\frac{1}{2a}ln|\frac{x-a}{x+a}|+C[/m] [/r] во втором интеграле [m] a^2=\frac{9}{4}[/m] ⇒ [m] a=\frac{3}{2}[/m]
[m]=\frac{3}{2}∫ \frac{du}{u}-\frac{7}{2}∫ \frac{1}{t^2-(\frac{3}{2})^2}dt=[/m]
[m]=\frac{3}{2}ln|u|-\frac{7}{2}\cdot \frac{1}{2\cdot \frac{3}{2}}ln|\frac{t- \frac{3}{2}}{t+ \frac{3}{2}}|+C=[/m]
[m]=\frac{3}{2}ln|x^2+5x+4|-\frac{7}{6}ln|\frac{x+\frac{5}{2}- \frac{3}{2}}{x+\frac{5}{2}+ \frac{3}{2}}|+C=[/m]
[m]=\frac{3}{2}ln|(x+1)(x+4)|-\frac{7}{6}ln|\frac{x+1}{x+4}|+C=[/m] Это ответ.
Но можно его преобразовать, применив свойства логарифма произведения и частного:
[m]=\frac{3}{2}ln|x+1|+\frac{3}{2}ln|x+4|-\frac{7}{6}ln|x+1|+\frac{7}{6}ln|x+4|+C=[/m]
[m]=\frac{3}{2}ln|x+1|-\frac{7}{6}ln|x+1|+\frac{3}{2}ln|x+4|+\frac{7}{6}ln|x+4|+C=[/m]
[m]=\frac{2}{6}ln|x+1|+\frac{16}{6}ln|x+4)|+C=\frac{1}{3}ln|x+1|+\frac{8}{3}ln|x+4|+C=\frac{1}{3}ln(x+1)\cdot(x+4)^{8}+C=[/m]
[m]=ln\sqrt[3]{(x+1)(x+4)^8}+C[/m]