Задача 61271 Решить неоднородную систему ОДУ ...
Условие
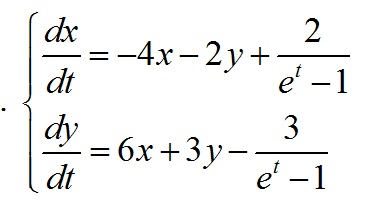
Решение
[m]\left\{\begin {matrix}x`(t)=-4x-2y+\frac{2}{e^{t}-1}\\y`(t)=6x+3y-\frac{3}{e^{t}-1}\end {matrix}\right.[/m]
Выразим из первого уравнения y и подставим во второе уравнение:
[m]\left\{\begin {matrix}y=-\frac{1}{2}x`(t)-2x+\frac{1}{e^{t}-1}\\(-\frac{1}{2}x`-2x+\frac{1}{e^{t}-1})`=6x+3\cdot(-\frac{1}{2}x`-2x+\frac{1}{e^{t}-1} )-\frac{3}{e^{t}-1}\end {matrix}\right.[/m]
Решаем второе уравнение:
[m](-\frac{1}{2}x`-2x+((e^{t}-1)^(-1))`=6x+3\cdot(-\frac{1}{2}x`-2x+\frac{1}{e^{t}-1} )-\frac{3}{e^{t}-1}[/m]
[m](-\frac{1}{2}x`-2x+(-1)\cdot (e^{t}-1)^{-2} \cdot (e^{t}-1)`=6x+3\cdot(-\frac{1}{2}x`-2x+\frac{1}{e^{t}-1} )-\frac{3}{e^{t}-1}[/m]
[m]-\frac{1}{2}x``-2x`-\frac{e^{t}}{(e^{t}-1)^2}=6x-\frac{3}{2}x`-6x+\frac{3}{e^{t}-1}-\frac{3}{e^{t}-1}[/m]
Получили линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами
[m]x``+x`=-\frac{2e^{t}}{(e^{t}-1)^2}[/m]
Решаем однородное уравнение:
[m]x``+x`=0[/m]
Cоставляем характеристическое уравнение:
k^2+k=0
k_(1) = 0; k_(2)=-1
Общее решение однородного уравнения имеет вид:
[m]y=C_{1}+C_{2}e^{-t}[/m]
Правая часть[m] f(t)=-\frac{2e^{t}}{(e^{t}-1)^2}[/m] не является функцией специального вида.
Решаем методом вариации произвольных постоянных
[m]y=C_{1}(t)+C_{2}(t)e^{-t}[/m]
C_(1) x и С_(2)(х) находим из системы:
[m]\left\{\begin {matrix}C’_{1}(t)+C`_{2}(t)\cdot e^{-t}=0\\C`_{1}(t)\cdot (1)`+C’_{2}(t)\cdot (e^{-t})`=-\frac{2e^{t}}{(e^{t}-1)^2}\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}C’_{1}(t)=-C`_{2}(t)\cdot e^{-t}\\C`_{1}(t)\cdot 0+C’_{2}(t)\cdot (-e^{-t})=-\frac{2e^{t}}{(e^{t}-1)^2}\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}C’_{1}(t)=-C`_{2}(t)\cdot e^{-t}\\-C’_{2}(t)\cdot e^{-t}=-\frac{2e^{t}}{(e^{t}-1)^2}\end {matrix}\right.[/m] ⇒
[m]\left\{\begin {matrix}C’_{1}(t)=-C`_{2}(t)\cdot e^{-t}\\C’_{2}(t) =\frac{2}{(e^{t}-1)^2}\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}C’_{1}(t)=-C`_{2}(t)\cdot e^{-t}\\C_{2}(t) = ∫ \frac{2}{(e^{t}-1)^2}dt\end {matrix}\right.[/m]
[m]C_{2}(t) = ∫ \frac{2}{(e^{t}-1)^2}dt[/m] применяем метод замены переменной:
[m] e^{t}-1=u[/m] ⇒ [m] e^{t}=u+1[/m] ⇒ [m]t=ln(u+1)[/m] и [m]dt=\frac{1}{u+1}du[/m]
тогда
[m]C_{2}(t) = ∫ \frac{2}{u^2}\cdot\frac{1}{u+1}du [/m]
Раскладываем подинтегральную дробь на простейшие
[m] \frac{2}{u^2(u+1)}=\frac{A}{u}+\frac{B}{u^2}+\frac{D}{u+1} [/m]
[m]2=A\cdot u(u+1)+B\cdot (u+1)+D\cdot u^2[/m]
⇒
[m]B=2[/m]
[m]A+B=0[/m] ⇒ [m]A=-B=-2[/m]
[m]A+D=0[/m] ⇒ [m]D=-A=2[/m]
[m] \frac{2}{u^2(u+1)}=-\frac{2}{u}+\frac{2}{u^2}+\frac{2}{u+1} [/m]
[m]C_{2}(t) = ∫(-\frac{2}{u}+\frac{2}{u^2}+\frac{2}{u+1})du [/m]
[m]C_{2}(t) = -2ln|u|-\frac{2}{u}+2ln|u+1|+C_{3} [/m]
Обратная замена:
[m] u=e^{t}-1[/m] ⇒ [m] u+1=e^{t}[/m] ⇒ [m]ln(u+1)=t[/m]
[m]C_{2}(t) = -2ln|e^{t}-1|-\frac{2}{e^{t}-1}+2t+C_{3} [/m]
Находим
[m]C’_{1}(t)=-C`_{2}(t)\cdot e^{-t}[/m]
[m]C’_{1}(t)=-(-2ln|e^{t}-1|-\frac{2}{e^{t}-1}+2t+C_{3})\cdot e^{-t}[/m]
Интегрируем:
[m]C_{1}(t)= ∫( 2ln|e^{t}-1|-\frac{2}{e^{t}-1}+2t+C_{3})\cdot e^{-t}dt[/m]...
....